Сложные ставки ссудных процентов
Если после очередного интервала начисления доход (то есть на численные за данный интервал проценты) не выплачивается, то он присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.
Обозначения:
ic – относительная величина годовой ставки сложных ссудных процентов;
kн.с – коэффициент наращения в случае сложных процентов;
j – номинальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).
Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (11.12), составит:
| S1 = P (l+ ic.). | (11.30) |
Еще через год это выражение применяется уже к сумме S1:
| S2 = S1(l+ ic ) = P (l+ ic)2 | (11.31) |
и так далее. Следовательно, что по прошествии n лет наращенная сумма составит:
| S = P (1 + ic) n. | (11.32) |
Множитель наращения kн.с соответственно будет равен:
| kн.с = (1 + iс)n. | (11.33) |
При начислении простых процентов он составил бы по формулам (11.10) и (11.12):
| kн.с = (1 + n). | (11.34) |
Сравнивая два последних выражения для коэффициентов наращения, можно видеть, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов.
Если срок ссуды п в годах не является целым числом, множитель наращения определяют по выражению:
| kн.с = (1+ ic) na (1 + nb ic ), | (11.35) |
где п = па + пb; nа — целое число лет; пb – оставшаяся дробная часть года.
На практике предпочитают пользоваться формулой (11.32) с соответствующим нецелым показателем степени. Но нужно иметь в виду, что с точки зрения сущности начисления процентов этот способ является приблизительным, и погрешность при вычислениях будет тем больше, чем больше значения входящих в формулу величин. Наибольшее расхождение можно получить при nb = 1/2, в этом случае удобно применить формулу (11.32). Следует учитывать, что приблизительный метод дает меньший, чем в действительности, результат. Следовательно, когда номиналы денежных сумм достаточно велики, от этого метода лучше отказаться вовсе.
Если предположить, что уровень ставки сложных процентов будет разным на различных интервалах начисления: n1, п2, ..., пN – продолжительность интервалов начисления в годах; i1, i2, ..., iN − годовые ставки процентов, соответствующие данным интервалам. Тогда наращенная сумма в конце первого интервала начисления в соответствии с формулой (11.12), составит:
| S1= P (l+ n1 i1). | (11.36) |
В конце второго интервала:
| S2= P (l+ n1 i1) ×(l+ n2 i2 ). | (11.37) |
При N интервалах начисления наращенная сумма в конце всего периода начисления составит:
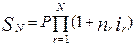 . .
| (11.38) |
Если все интервалы начисления одинаковы (как и обычно на практике) и ставка сложных процентов одна и та же, формула (11.38) принимает вид:
| SN = P (l+ n i ) n . | (11.39) |
В случае, если начисление сложных процентов осуществляется один раз в году, оговариваетсяноминальная ставка процентов j – годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления. При т равных интервалах начисления и номинальной процентной ставке j эта величина считается равной j/m.
Если срок ссуды составляет п лет, то, аналогично формуле (11.32), получаем выражение для определения наращенной суммы:
| Smn = P (l+ j/m) mn , | (11.40) |
где mn − общее число интервалов начисления за весь срок ссуды.
Если общее число интервалов начисления не является целым числом (тп – целое число интервалов начисления; l – часть интервала начисления), то выражение (11.40) принимает вид
| S = P ( l+ j/m) mn (l + l j/m). | (11.41) |
Для целого числа периодов начисления используется формула сложных процентов (11.32), а для оставшейся части – формула простых процентов (11.12).
В России в настоящее время наиболее распространенным является начисление процентов по полугодиям, поквартальное и ежемесячное (иногда интервалом начисления может являться и день). Такие проценты, начисляемые с определенной периодичностью, называются дискретными [74, 83].
В мировой практике часто применяется также непрерывное начисление сложных процентов (продолжительность интервала начисления стремится к нулю, a m – к бесконечности) [83].
В этом случае для вычисления наращенной суммы служит следующее выражение:
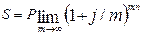 . .
| (11.42) |
Для расчетов наращенной суммы можно использовать известную формулу:
| S= Ре jn, | (11.43) |
где
| kн.с = е jn. | (11.44) |
Значения наращенной суммы S можно вычислять с помощью финансового калькулятора или находя значения еjn и других требуемых величин в специальных таблицах.
Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях (при одинаковых n, j, Р).
Аналогично случаю простых процентов полученные формулы можно преобразовывать, выражая одни величины через другие в зависимости от того, что известно, а что требуется найти. Так, из формулы (11.32) получаем:
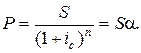
| (11.45) |
В случае простых процентов определение современной величины суммы S называется дисконтированием.
Коэффициент дисконтирования а является величиной, обратной коэффициенту наращения, то есть k н.сα = 1.
Формула (11.45), а также соответствующие формулы для случая простых ставок ссудного процента и для учетных ставок показывают, чтотекущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности [8, 74, 83].
Также из формулы (11.32) получим:
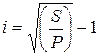 . .
| (11.46) |
Из формулы (10.35):
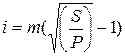 . .
| (11.47) |
Применяя операцию логарифмирования к обеим частям формулы (11.32), получаем:
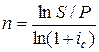 . .
| (11.48) |
Подобным же образом из формулы (10.35) получаем формулу:
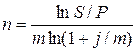
| (11.49) |
Дата добавления: 2017-06-02; просмотров: 909;
