Весовой стабилизирующий момент при комбинированном наклоне шкворня

Предположим, что цапфа управляемого колеса, имеющего только поперечный наклон шкворня a_ш, имеет возможность поворота вокруг оси шкворня на угол Q>90⁰. В этом случае весовой стабилизирующий момент от поперечного наклона шкворня можно определить по формуле (9.11).

Проведём расчёт весового стабилизирующего момента от поперечного наклона шкворня, используя исходные данные автомобиля КрАЗ-260: Rz=27282 Н; l_ц = 0,225м; r_к = 0,6м; a_ш=9⁰30^/, g_ш0=-0⁰30^/. Результаты расчётов момента по формуле (9.11) в полном диапазоне углов поворота цапфы для левого управляемого колеса представлены на рис. 9.8 кривой 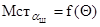. 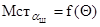Из анализа рис.9.8 следует, что при повороте цапфы от нейтрального положения до 90⁰ весовой стабилизирующий момент от поперечного наклона шкворня возрастает от нуля до максимального значения. При дальнейшем повороте на угол Q>90⁰ весовой стабилизирующий момент уменьшается.

Следовательно, угол поперечного наклона шкворня a_ш после поворота управляемого колеса от нейтрального положения на 90⁰ по отношению к колесу становится эквивалентным углу продольного наклона шкворня b_ш = a_ш. Очевидно, что и весовой стабилизирующий момент от поперечного наклона шкворня при угле поворота цапфы на угол 90⁰ от нейтрального положения с учётом проведенных рассуждений равен весовому стабилизирующему моменту от продольного угла наклона шкворня при угле поворота цапфы Q=0 и при равенстве углов a_ш = b_ш.

Что касается знака, то весовой стабилизирующий момент от поперечного наклона шкворня всегда возвращает колесо к нейтральному положению, а поэтому, с учетом принятых допущений, будет положительным. Весовой момент от продольного наклона шкворня имеет разный знак в зависимости от направления поворота цапфы управляемого колеса. Так, для правого управляемого колеса он будет положительным при повороте вправо от положения, соответствующего прямолинейному движению автомобиля, а для левого колеса – влево. В противном случае момент будет отрицательным.

С учётом изложенного на рис.9.8 приведена кривая 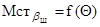в диапазоне

углов поворота цапфы вправо и влево на 30⁰. Она получена переносом кривой 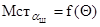в диапазоне углов поворота цапфы от положения 90⁰ вправо и влево на 30⁰ . Заштрихованная зона соответствует отрицательному значению стабилизирующего момента. Просуммировав значения 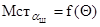и 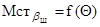при соответствующих углах поворота цапфы Q, получаем кривую весового стабилизирующего момента от комбинированного наклона шкворня 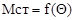(см. рис. 9.8).

Следовательно, зная зависимость весового стабилизирующего момента 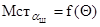при поперечном наклоне шкворня и учитывая приведенные рассуждения, можно графически получить зависимость 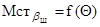при продольном наклоне шкворня, а затем зависимость 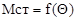при комбинированном наклоне шкворня.

Из анализа кривой 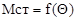видно, что для левого управляемого колеса при повороте влево весовой стабилизирующий момент положительный и возвращает колесо к нейтральному положению. Однако при повороте вправо он имеет отрицательное значение, направлен в сторону от нейтрального положения и в данном случае достигает минимального значения при правом крайнем положении.

Изложенная взаимосвязь между влиянием продольного и поперечного наклонов шкворня на величину и направление действия весового стабилизирующего момента даёт возможность формулы, полученные для определения весового стабилизирующего момента от поперечного наклона шкворня, применить для определения этого момента от продольного и комбинированного наклонов шкворня.

Вектор весового стабилизирующего момента, обусловленного комбинированным наклоном шкворня, определим по формуле

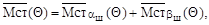(9.14)

где 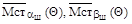- векторы весовых стабилизирующих моментов, обусловленные соответственно поперечным и продольным наклонами шкворня.

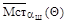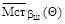Так как векторы и направлены вдоль оси шкворня, то абсолютное значение весового стабилизирующего момента при комбинированном наклоне шкворня с учётом направления действия будет определяться зависимостью

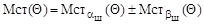. (9.15)

Неизвестной величиной в зависимости (9.15) является момент 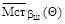. Учитывая вышеприведенную взаимосвязь между наклонами шкворня и углом поворота управляемого колеса, вправе записать

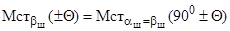. (9.16)

С учётом формулы (9.11) весовой стабилизирующий момент от поперечного наклона шкворня a_ш при угле поворота цапфы управляемого колеса на угол 90⁰±Q можно определить так

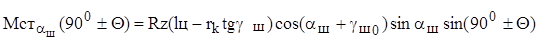. (9.17)

С учетом зависимостей (9.16) и (9.17), а также, учитывая направление действия весового стабилизирующего момента, этот момент от продольного наклона шкворня равен

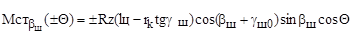. (9.18)

Подставив в формулу (9.15) выражения (9.17) и (9.18) и проведя несложные преобразования, получим зависимость весового стабилизирующего момента от угла поворота колеса при комбинированном наклоне шкворня 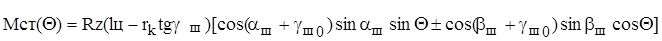. (9.19)

Неизвестной величиной в формуле (9.19) является 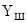- текущий угол развала управляемого колеса, обусловленным комбинированным наклоном шкворня. Его значение определим по формуле

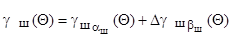(9.20)

где 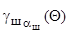- текущий угол развала при поперечном наклоне шкворня, который определяется по формуле (9.13);

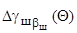- приращение текущего угла развала от продольного наклона шкворня, которое определяется так

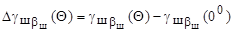, (9.21)

где 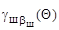, 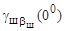- текущие углы развала колеса, вызванные продольным наклоном шкворня при углах поворота цапфы соответственно Q и 0⁰.

Используя взаимосвязь углов наклонов шкворней с углом поворота цапфы управляемого колеса, запишем ,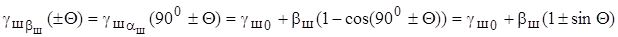

(9.22)

где 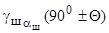- текущий угол развала управляемого колеса, вызванный поперечным наклоном шкворня при угле поворота его цапфы на угол 90⁰±Q.

Воспользовавшись зависимостью (9.22), определим текущий угол развала от продольного наклона шкворня при угле поворота цапфы на 0⁰

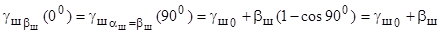. (9.23)

После подстановки (9.22) и (9.23) в выражение (9.18) получим приращение текущего угла развала от продольного наклона шкворня при повороте цапфы на угол Q от нейтрального положения.

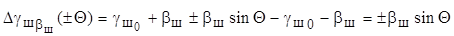. (9.24)

Окончательно текущий угол развала управляемого колеса при комбинированном наклоне шкворня определяется следующим выражением

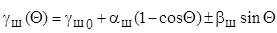. (9.25)

Заметим, что в формулах (9.19) и (9.25) знак “плюс” необходимо брать при повороте цапфы левого колеса влево от нейтрального положения, а правого- вправо. В противном случае нужно брать знак “минус”.

Литература

1. Литвинов А.С., Фаробин Я.Е. Автомобиль:Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-151…155.

2. Солтус А.П., Кошарный Н.Ф. К вопросу о весовых стабилизирующих моментах. Ж.»Автомобильная промышленность».-М.,1976.-№8.

3. Солтус А.П. Основы теории рабочего процесса и расчета колесных управляющих модулей (монография). Деп.Укр.НИИНТИ.№501-Ук90 ВИНИТИ «Деп.науч.труды»,1990, №7 (290),б/о 203.-234с., с.- 85-115

4.Солтус А.П., Черненко С.М. Визначення вагового стабілізуючого моменту, викликаного поперечним нахилом шворня. Машинознавство.- Львів:-2002, №7(61), с.46-51

5. Солтус А.П., Черненко С.М. Определение весового стабилизирующего момента от комбинированного наклона шкворня. Автомобильный транспорт. Сб. науч. тр.-Харьков, ХГАДТУ:-2003, вып. 12.-с.23-26.

Контрольные вопросы

1.Что такое поперечный, продольный и комбинированный наклоны шкворня?

2. Чем вызван весовой стабилизирующий момент?

3. Как называется звено, соединяющее управляемое колесо со шкворнем?

4.Что такое текущий угол развала колеса?

5. Как изменяется весовой стабилизирующий момент от поперечного наклона шкворня в зависимости от угла поворота колеса?

6.Какая существует связь между поперечным, продольным наклонами шкворня и углом поворота колеса?

7.При каком угле поворота колеса весовой стабилизирующий момент от продольного наклона шкворня достигает максимального значения?

8. Что обозначает знак весового стабилизирующего момента?