Весовой стабилизирующий момент при поперечном наклоне шкворня

Поворот управляемых колёс автомобилей осуществляется вокруг осей, которые принято называть осями шкворней. В общем случае эти оси имеют наклон в двух взаимно перпендикулярных плоскостях – поперечной (боковой наклон) и продольной. Такой наклон называется комбинированным наклоном шкворня. Из-за наклонов шкворней, конструктивных параметров управляемого моста и колёс возникает момент, вызванный весом, приходящимся на управляемое колесо. Поскольку он зависит от веса, его называют весовым. Величину и направление этого момента необходимо знать при проектировании механизмов рулевых управлений автомобилей, так как он является составной частью момента сопротивления повороту колёс как на месте, так и при движении, а также при исследовании колебаний управляемых колёс, поскольку при колебании колёса поворачиваются вокруг осей шкворней.

При определении весового стабилизирующего момента были приняты следующие допущения:

-изменениями углов наклонов шкворня и нагрузки на управляемое колесо, обусловленных перекосом переднего моста при повороте колёс пренебрегаем и считаем их постоянными;

-равнодействующая нормальных реакций опорной поверхности Rz приложена в точке пересечения плоскости симметрии обода с малой осью контактного отпечатка и не зависит от текущего угла развала;

-весовой стабилизирующий момент считаем положительным, если при фиксированном положении колеса он направлен так, что возвращает его в положение прямолинейного движения. В противном случае считаем момент отрицательным. Это позволит в формулах учесть направление действия весового стабилизирующего момента.

Вначале рассмотрим определение весового стабилизирующего момента только от поперечного наклона шкворня. В общем случае для определения весового стабилизирующего момента существует три способа: классической механики (произведение силы на плечо), аналитической геометрии (векторное произведение двух векторов) и закон сохранения энергии. В качестве примера, рассмотрим определение весового момента способом классической механики.

Согласно классической механики весовой стабилизирующий момент Мст запишем как произведение силы на плечо ее действия относительно оси шкворня

Мст = F × l , (9.9)

где F – сила, перпендикулярная оси шкворня;

l – расстояние от оси шкворня до вектора силы F.

Схема для определения весового стабилизирующего момента способом классической механики приведена на рис.9.6. Согласно рис.9.6 приняты следующие обозначения: r_к – радиус колеса; l_ц – длина цапфы; a_ш – угол поперечного наклона шкворня; g_ш0 – угол развала колеса в положении прямолинейного движения; Rz – равнодействующая нормальных реакций опорной поверхности, вызванная весом, приходящимся на колесо.

Анализ конструкций управляемых мостов автомобилей показал, что между управляемым мостом и осью шкворня существует промежуточное звено цапфа (см. рис.9.6).

Цапфа вращается вокруг оси шкворня, который может быть закрепленным на балке моста неподвижно при помощи штифта, конуса со шпонкой (автомобили неполноприводные) или на полноприводных автомобилях поворачивается на конических подшипниках вокруг шаровой опоры. Следовательно, цапфа является рычагом, закрепленным на оси шкворня.

Силой, приложенной к этому рычагу, и создается момент относительно оси шкворня. Поскольку такой силой является равнодействующая нормальных реакций R_z, создаваемая весом на управляемое колесо, поэтому эту равнодействующую перенесем по линии ее действия до оси цапфы в точку А.

Рис 9.6 Схема для определения весового стабилизирующего момента способом классической механики

Учитывая, что момент относительно оси создается силой перпендикулярной этой оси, разложим равнодействующую на две составляющие: Rz×sina_ш – перпендикулярную оси шкворня и Rz×cosa_ш – параллельную оси шкворня.

Очевидно, что в выражении (9.9) силой F будет составляющая Rz×sina_ш. Для определения момента необходимо определить плечо действия силы Rz×sin a_ш относительно оси шкворня.

Для этого из точки А опустим перпендикуляр на ось шкворня. Полученная таким образом точка О является центром, относительно которого будет вращаться точка А.

При повороте цапфы колеса на угол Q точка А займёт положение точки А^/, а расстояние А^/Д и будет плечом l, на котором создается весовой стабилизирующий момент.

Из анализа ∆СДА^/ имеем А^/Д = l = А^/ОsinQ.

Из ∆ОАС, учитывая, что А^/О= АО, запишем

АО = AC cos (a_ш+g_ш0).

Из анализа рис.9.6 следует, что

АС = ВС – АВ = l_ц – r_кtg g_ш,

где g_ш - текущий угол развала управляемого колеса.

Тогда l = (l_ц – r_кtg g_ш) cos (a_ш+g_ш0) sin Q. (9.10)

После подстановки (9.10) в выражение (9.9), а вместо силы F ее значение получим окончательно

Мст( 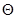) = Rz×sin a_ш(l_ц – r_кtg g_ш) cos (a_ш+g_ш0) sin Q. (9.11)

Неизвестной величиной в формуле (9.11) является текущий угол развала. Расчетная схема для определения текущего угла развала левого управляемого колеса приведена на рис.9.7.

Из анализа рис.9.7 следует, что при повороте колеса вокруг оси шкворня его центр (точка В) будет перемещаться по дуге окружности с центром в точке О и радиусом ОВ. Если цапфа повернется на угол Q, тогда точка В опустится на величину FG и займет положение В^/=Е.Текущий угол развала равен g_ш = ÐCВ^/G.

Из анализа ∆CВ^/G sin g_ш = CG/CB^/ = CG/l_ц, поскольку ВС = В^/С = l_ц .

Из анализа рис.9.7 запишем CG = CF + FG,

где CF = l_ц ∙ sin g_ш0 и FG = BВ^/ ∙ sin a_ш.

Если учесть, что BВ^/ =ВЕ, тогда из рис.9.7 следует, что

BE = BO-EO = l_ц ∙cos (a_ш+g_ш0)∙(1-cos Q).

Подставив полученные значения в уравнение синуса текущего угла развала, после элементарных преобразований получим

sin g_ш = sin g_ш0 + cos (a_ш+g_ш0)∙(1-cos Q) ∙sin a_ш (9.12)

Таким образом, используя зависимости классической механики, получены зависимости (9.11) и (9.12) для определения весового стабилизирующего момента и текущего угла развала.

Если учесть, что при малых углах sin g_ш=g_ш, sin g_ш0=g_ш0 , sin a_ш=a_ш,

cos (a_ш+g_ш0)=1, тогда выражение (9.12) примет вид

g_ш( 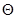)=g_ш0+a_ш(1-cos Q) . (9.13)