Расчет волатильности

Стандартное отклонение (среднеквадратическое отклонение) или историческая волатильность:

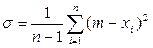, (5)

где σ – стандартное отклонение, или историческая волатильность; n – количество наблюдений (количество баров, свечей в рассматриваемом периоде); m – среднее арифметическое; x_i – изменения цены.

Среднее равно

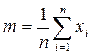. (6)

При анализе ценового риска на финансовых рынках, например при расчете волатильности акции принято работать не с самой последовательностью цен, а с последовательностью относительных изменений [6, 11, 17].

Последовательность относительных изменений имеет ряд преимуществ по сравнению с последовательностью цен.

Во-первых, преобразование последовательности цен в последовательность относительных изменений позволяет получить большую сравнимость различных последовательностей цен (различных активов). Например, новые акции (IPO) могут расти и падать за короткий период в десятки раз, поэтому при расчете волатильности таких акций нельзя использовать абсолютные значения.

Во-вторых, последовательность относительных изменений отличается большей стабильностью в том смысле, что для нее среднее и дисперсия в большей степени являются стационарными, чем среднее и дисперсия последовательности «необработанных» цен. Относительные изменения рассчитывают двумя путями [11]:

– как процентное изменение цены:

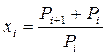; (7)

– в качестве переменной величины принимают логарифм отношения последующей цены к цене предыдущей (обычно это цены закрытия), т.е. x_i равен натуральному логарифму ценового изменения:

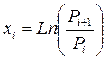. (8)