Факторы, влияющие на дюрацию

Дюрация меняется по мере выплаты купонов держателю облигации. Поскольку держатель облигации получает купонную выплату, сумма денежного потока уже не входит во временной промежуток, это значит, что эта выплата больше не учитывается как будущий денежный поток, который идет на возмещение держателю облигации.

При выплате первого купона (рис. 7) уровень теряет равновесие, поскольку купонная выплата больше не учитывается [20].

Рис. 7. Изменение дюрации при купонных выплатах

Дюрация увеличивается сразу же в день купонной выплаты, но в течение жизни облигации дюрация продолжает уменьшается, поскольку уменьшается время погашения облигации. У первой диаграммы на рис. 7 пять периодов выплаты, а у второй диаграммы только четыре. Однако это сокращение временного промежутка происходит постепенно, а поскольку это все-таки происходит, дюрация снова и снова уменьшается [20].

Дюрация уменьшается по мере того, как время приближается к сроку погашения. Дюрация также мгновенно увеличится в день выплаты и удаления купона из серии будущих денежных потоков. Это происходит до тех пор, пока дюрация не сойдется в одной точке со сроком погашения облигации.

На дюрацию также влияют процентная ставка облигации и ее доходность. Облигации с высокими купонными ставками и соответственно высокой доходностью будут стремиться к более низким дюрациям, чем облигации с низкой ставкой или низкой доходностью.

Волатильность цены облигации

Под волатильностью (изменчивостью)цены облигациипонимается реакция цены облигации на мгновенное, скачкообразное изменение ее доходности к погашению при прочих равных условиях [11, 17, 20].

Реакция цены облигации на изменение требуемой доходности имеет ряд характерных признаков:

1. Зависимость между доходностью к погашению (YTM)1и рыночной ценой облигации носит обратный характер.

2. Чем выше купонная ставка, тем слабее реагирует цена облигации на одни и те же изменения доходности к погашению при одинаковых сроках погашения. Соответственно, чем ниже купонная ставка, тем сильнее реакция цены на одни и те же изменения доходности к погашению.

3. Если купонная ставка процента не меняется, то увеличение срока погашения облигации вызывает более сильную реакцию цены P облигации на одни и те же изменения ее доходности к погашению.

4. Небольшие изменения доходности к погашению приводят к одинаковым изменениям цены облигации в обоих направлениях. Иными словами, если доходность к погашениювозрастаетна незначительную величину, то это приводит к такому процентному уменьшениюцены P, которое приблизительно будет равно процентному повышению P при таком же незначительном снижении YTM.

5. Значительные изменения доходности к погашению вызывают асимметрическую реакцию цен облигации: если доходность к погашению возрастаетна несколько процентов (например, 2 %), то вызванное этим снижениецены облигации будет в процентном отношении меньшепо абсолютной величине процентного приращенияцены облигации при снижениидоходности к погашению на те же 2 %.

6. При заданном уровне изменения доходности к погашению имеем следующее: чем ниже исходная доходность к погашению, тем выше реакция цены на ее изменения.

Доходность к погашению (YTM) – это процентная ставка в коэффициенте дисконтирования, которая устанавливает равенство между текущей стоимостью потока платежей по облигации и её рыночной ценой P [19, 21]:

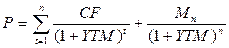, (9)

где CF – поток купонных выплат; М – номинальная цена облигации; YTM – доходность к погашению.

Если процентная ставка поднимается, то цена облигации падает и наоборот. Как правило, у облигаций с высокой дюрацией колебание цены будет выше, чем у облигаций с низкой дюрацией. На волатильность цены облигации большое влияние оказывают пять факторов [20]:

а) уровень доходности к погашению;

б) размах изменений доходности к погашению;

в) направления этих изменений;

г) величина купонной ставки;

д) срок погашения.

Чувствительность цены облигации к изменениям процентных ставок определяются тремя основными факторами: купонной ставкой, сроком погашения и доходностью к погашению.

Факторы 1 и 2: купонная ставка и срок погашения. Если срок погашения и первоначальная цена облигации остаются постоянными, то чем выше купон, тем ниже волатильность, и чем ниже купон, тем выше волатильность. Если купонная ставка и первоначальная цена облигации остаются постоянными, облигация с более длительным сроком погашения будет отображать более высокую волатильность цены, а облигация с более коротким сроком погашения будет отображать более низкую волатильность цены. Таким образом, если инвестировать в облигацию с минимальным риском процентной ставки, то самой оптимальной будет облигация с высокими купонными выплатами и коротким сроком погашения [9, 50].

Фактор 3: доходность к погашению. Облигация с высокой доходностью к погашению будет отображать более низку волатильность цены, чем облигация с более низкой доходностью к погашению, но при равной купонной ставке и сроке погашения. Кредитный рейтинг облигации также оказывает влияние на доходность к погашению. У облигаций с низкими кредитными рейтингами будет более высокая доходность, чем у облигаций с высокими кредитными рейтингами.

Следовательно, для облигаций с низкими кредитными рейтингами характерна более низкая волатильность цены, чем у облигаций с высокими кредитными рейтингами [17, 20]. Если облигация обладает и коротким сроком погашения, и низкой купонной ставкой, то ее характеристики будут иметь обратный эффект на ее волатильность: низкий купон поднимется, а короткий срок погашения снизит волатильность. Тогда волатильность облигации будет средним от этих двух противоположных эффектов.

Типы дюраций

На сегодняшний день существует четыре типа дюрации [6, 11, 23]:

– Маколея,

– модифицированная,

– эффективная,

– на основе ключевых процентных ставок.

Текущая рыночная цена P₀ облигации, имеющей m купонных выплат в год, определяется по формуле

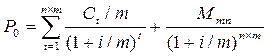, (10)

где С – годовые процентные выплаты, определяющиеся номинальным процентным доходом (купонной ставкой); i – требуемая норма доходности; m – частота выплат процентов в году; i/m – величина доходности к погашению; C_t/m – купонные выплаты; M_mn – номинал облигации; n – число лет до погашения облигации.

1. Дюрация Маколея

Дюрация Маколея – средневзвешенный срок до погашения потоков наличности от облигации, в котором в качестве весов выступают текущие стоимости потоков наличности, деленные на цену [9, 20].

Дюрация любой облигации высчитывается по формуле

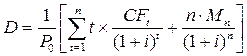, (11)

где CF_t – денежный поток в момент времени t; P₀ - рыночная цена облигации;

t – период времени, в течение которого поступает денежный поток, t=1, 2, .., n лет; денежный поток в момент t составляют купонные выплаты C_t и номинал M_n; n – количество лет, в течение которых поступают купонные выплаты; i – годовая доходность к погашению. Иначе:

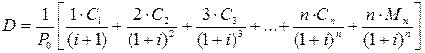. (12)

Если начисление купонных выплат производится раз в полгода, то в этом случае величина длительности удваивается. Длительность бескупонных облигаций оценивается следующим образом. Так как для этих облигаций все величины С_t=0, то

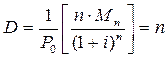. (13)

Следовательно, длительность бескупонных облигаций всегда равняется сроку погашения этой облигации – n лет.

Дюрация Маколея высчитывается путем сложения результатов, полученных при умножении текущей цены каждого денежного потока на время его получения, деленных на стоимость ценной бумаги. Дюрация Маколея равна

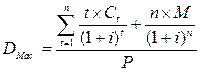, (14)

где n – количество денежных потоков; t – время до погашения; C – денежный поток; i – требуемая доходность; M – номинальная стоимость облигации; P – цена облигации.

2. Модифицированная дюрация

Модифицированная дюрация является модифицированной версией модели Маколея, которая учитывает изменение процентной ставки. Поскольку процентная ставка влияет на доходность, то ее колебание повлияет и на дюрацию.

Модифицированная дюрация показывает, как она меняется при изменении доходности на 1 % [17, 18, 20]. Для облигаций без особенностей встроенного опциона1 цена облигации и процентная ставка движутся в обратном направлении, то есть существует обратная связь между модифицированной дюрацией и изменением доходности на 1 %.

Модифицированная дюрация показывает, как изменяется дюрация облигации по отношению к движениям процентной ставки. Формула (13) может применяться для расчета волатильности какой-то конкретной облигации. Модифицированная дюрация рассчитывается по формуле

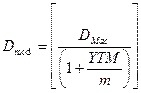, (15)

где YTM – доходность к погашению; m – количество купонных выплат в год.

Формула показывает, как будет меняться дюрация, если процентная ставка поднимется на 100 базисных пунктов. Модифицированная дюрация всегда будет ниже, чем дюрация Маколея.

3. Эффективная дюрация

Формула модифицированной дюрации предполагает, что ожидаемые денежные потоки будут оставаться постоянными, даже если преобладающие процентные ставки изменятся.

С другой стороны, денежные потоки от ценных бумаг со встроенными опционами или с особенностями выкупа долговых обязательств будут меняться при изменении процентной ставки.

Для того чтобы высчитать дюрацию этих двух типов облигаций, самым уместным будет воспользоваться эффективной дюрацией. Эффективная дюрация требует использования биноминального дерева процентных ставок, чтобы высчитать спрэд с учетом опциона. Существует множество программ, доступных для инвесторов, желающих рассчитывать эффективную дюрацию.

4. Дюрация на основе ключевых процентных ставок

Дюрация на основе ключевых процентных ставок, при постоянном удерживании доходности для всех остальных погашений, позволяет рассчитывать дюрации портфеля при изменении на один базисный пункт процентных ставок. Дюрация на основе ключевых процентных ставок равна:

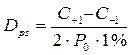, (16)

где С₊₁ – цена облигации после повышения доходности на 1 %; С_-1 – цена облигации после падения доходности на 1 %; P₀ – первоначальная цена облигации.

Чаще всего метод ключевого процента используется для таких портфелей, как «ступенчатая облигация», которая состоит из ценных бумаг с фиксированным доходом и с разными сроками погашения. Таким образом:

– если необходимый уровень дохода превышает установленную по облигации купонную ставку, то стоимость облигации будет ниже ее номинальной стоимости;

– если необходимый уровень дохода уступает установленной по облигации купонной ставке, то текущая стоимость облигации будет выше ее номинальной стоимости;

– если требуемый уровень дохода равен установленной по облигации процентной ставке, то текущая стоимость облигации будет равна ее номинальной стоимости.

Пример 1

Необходимо определить текущую стоимость облигации с оставшимся сроком до погашения 6 лет, номинальной стоимостью 100000 д.е., приносящей 6%-й купонный доход при требуемом уровне доходности 10 %.

Текущая стоимость основного долга (100000 д.е.), выплачиваемого в конце шестого года равна 56400 д.е. (100000 × 0,564).

Текущая стоимость аннуитета – 6000 д.е. (6 % от 100000 д.е.) в течение 6 лет под 10 % равна 26130 д.е. (5000 × 4355);

Текущая стоимость облигации равна 82530 д.е. (56400 + 26130).

Пример 2

Если вместо 10 %-го требуемого уровня доходности взять 4 %-й, то стоимость облигации будет следующая.

Текущая стоимость основного долга равна 79000 д.е. (100000 × 0,790).

Текущая стоимость аннуитета равна 31452 д.е. (6000 × 5242).

Текущая стоимость облигации равна 110452 д.е. (79000 + 31452).

Пример 3

Оценить текущую стоимость облигации нарицательной стоимостью 200000 д.е., купонной ставкой 15 % годовых и сроком погашения через 5 лет, если рыночная норма дохода 12 %. Процент по облигации выплачивается дважды в год.

При выплате же процентов по облигациям несколько раз в году уравнение (10) примет следующий вид:

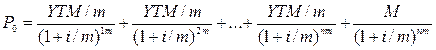, (17)

где m – частота выплат процентов в году.

Денежный поток в данном случае необходимо представить десятью периодами. Поскольку рыночная норма дохода составляет 12 %, то в расчете на полугодовой период она составит 6 %.

Текущая стоимость аннуитета 15000 д.е. (15 % от 200000 д.е.: 2) в течение 10 периодов под 6 % = 15000 × 7360 = 110400 д.е.

Текущая стоимость основного долга, выплачиваемого в конце 10 периода под 6 % = 200000 × 0,558 = 111600 д.е.

Текущая стоимость облигации = 110400 + 111600 = 222000 д.е.

Вопросы

1. Что такое «облигация»?

2. Какие виды облигаций вы знаете?

3. Что такое «дюрация облигаций»?

4. Как определяется дюрация традиционных облигаций?

5. Как рассчитывается дюрация Маколея?

Вексель

Вексель (от нем. Wechsel) – письменное долговое обязательство строго установленной формы, удостоверяющее ничем не обусловленное обязательство векселедателя (простой вексель), либо предложение иному указанному в векселе плательщику (переводный вексель) уплатить по наступлении предусмотренного векселем срока определенную денежную сумму [17, 31].

Вексель может быть ордерным, то есть передача прав по нему осуществляется путем совершения специальной надписи – индоссамента, или именным (передача прав производится по цессии). Индоссамент может быть бланковым (без указания лица, которому должно быть произведено исполнение) или именным (с указанием лица, которому должно быть произведено исполнение). Лицо, передавшее вексель посредством индоссамента, несет ответственность перед последующими векселедержателями за возможность осуществления прав по векселю.

Вексель выступает орудием коммерческого кредита. По своей форме векселя подразделяются на простые и переводные.

Простой вексель выписывается заемщиком. Переводной вексель (тратта) представляет собой письменный приказ кредитора заемщику об уплате последним определенной суммы третьему лицу (ремитенту). Наибольшее распространение получил переводный вексель. Форма векселя определяется законом страны, где он выписан. Вексель широко используется во внешней торговле в качестве средства оформления кредитно-расчетных отношений. Значительное распространение получили банковские акцепты (переводный вексель, выставленный на банк и им акцептованный).

По признаку эмитента различают:

– казначейские векселя – краткосрочные долговые обязательства, выпускаемые правительством страны обычно при посредничестве Центрального банка, со сроком погашения от 90 до 180 дней;

– частные векселя – эмитируются корпорациями, финансовыми группами, коммерческими банками. Вексель может обслуживать чисто финансовые и товарные сделки.

Первоначально векселедержателю запрещалось передавать свои права другим лицам, однако, когда эти ограничения стали сдерживающим фактором в торговле, и они были постепенно отменены. Вексельные права стало возможным передавать посредством проставления особого приказа векселедержателя – индоссамента (от лат. in – на и dorsum – спина, поскольку данная надпись совершалась, как правило, на обратной стороне векселя [23]).