Двух близких искусственных спутников.

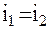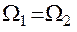Предположим, что два близких искусственных спутника обращаются по круговым орбитам с одинаковой угловой скоростью. Сразу заметим, что для проведения межспутниковых измерений на достаточно продолжительных временных интервалах эти предположения носят принципиальный характер, обеспечивая устойчивое движение системы. Совпадение плоскостей орбит спутников, т.е. выполнение условий и не обязательно. В этом случае для вывода уравнений наблюдений наряду с подходом, уже описанным в параграфе 4, возможно воспользоваться также разложением в ряд по степеням малого параметра, либо законом сохранения энергии.

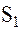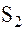Рассматривая систему двух искусственных спутников и , находящихся на расстоянии 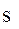друг от друга, разложим потенциал силы притяжения 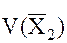в ряд Тейлора в окрестности потенциала :

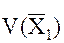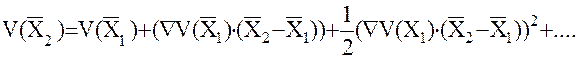
где 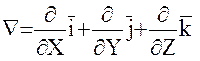- оператор Гамильтона, а 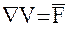- вектор силы притяжения. Близость спутников друг к другу позволяет ограничиться первым порядком разложения:

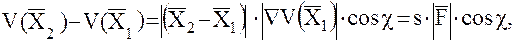
где 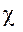- угол между направлениям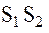и и 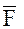. Окончательно

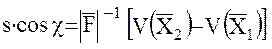. (37)

Равенство (37) может быть интерпретировано как уравнение наблюдений для измеряемых межспутниковых расстояний и направлений.

Одним из видов наблюдений в системе двух близких спутников является, как уже указывалось выше, относительная лучевая скорость 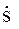, представляющая собой проекцию вектора относительной линейной скорости 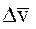на направление :

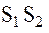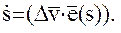
Вывод соответствующего измеряемой величине 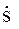уравнения наблюдений возможно осуществить, опираясь на закон сохранения энергии, в согласии с которым разность гравитационных потенциалов в точках 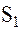и 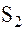равна разности кинетических энергий находящихся в этих точках спутников.

Предполагая, что движение спутников, массы которых примем за единицу, происходит лишь под действием силы притяжения Земли, запишем следующее равенство:

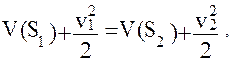
откуда имеем:

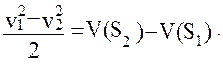(38)

Левая часть равенства (38) представляет собой разность кинетических энергий спутников, правая – разность гравитационных потенциалов Земли в точках 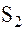и точках 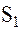. Перепишем (38) в виде:

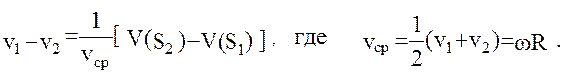
В первом приближении можно принять, что

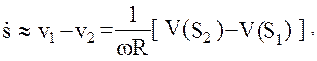(39)

рассматривая таким образом соотношение (39), связывающее результат измерения с искомой разностью потенциалов, как уравнение наблюдений для относительной лучевой скорости 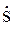. В ряде случаев, однако, высокая точность межспутниковых измерений требует установления более точной связи измеряемой и определяемых величин.

Наиболее просто поставленная задача может быть решена в случае обращения спутников по общей орбите (коорбитальное движение) на малом расстоянии друг от друга. При этом вместо (39) будем иметь:

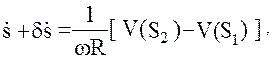(40)

где 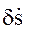- поправка, которую необходимо ввести в непосредственно измеренную относительную лучевую скорость 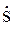. Введение указанной поправки обусловлено отличиями действительных положений и скоростей спутников от их номинальных положений и скоростей, соответствующих обращению по круговой опорной орбите. Вследствие этого, значение поправки 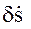должно быть вычислено по определяемым в ходе измерений векторам положений и скоростей элементов спутниковой системы. Оценки показывают, что прецизионная точность межспутниковых измерений предъявляет весьма жесткие требования к точности значений компонент векторов как абсолютных, так и относительных положений и скоростей самих искусственных спутников.