Двух близких искусственных спутников.
С практической точки зрения особенный интерес представляет исследование относительного движения двух искусственных спутников, движущихся на небольшом (по сравнению с удалением их от центра масс небесного тела) расстоянии друг от друга. Предположим, что компоненты вектора относительной дальности малы по сравнению с величиной 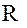 , т.е.
, т.е.

Тогда
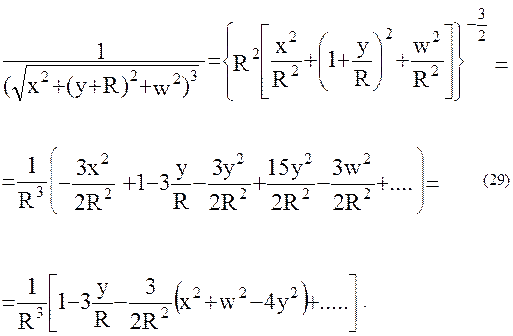
Подставляя (29) в (13), получаем:
 Ограничиваясь первым приближением, запишем систему (30) в виде
Ограничиваясь первым приближением, запишем систему (30) в виде
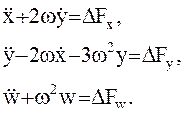 (31)
(31)
Система (31) имеет достаточно простое решение лишь при отсутствии возмущающих ускорений, т.е. 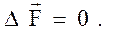 Тогда:
Тогда: 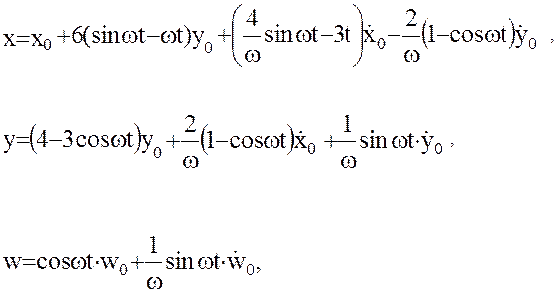
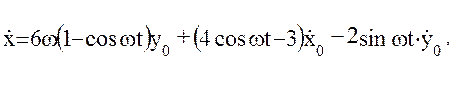 (32)
(32) 
 |
где
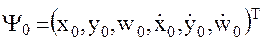 - вектор состояния относительного движения в начальный момент
- вектор состояния относительного движения в начальный момент 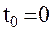 , а
, а 
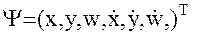 - вектор состояния относительного движения в текущий момент
- вектор состояния относительного движения в текущий момент 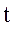 . Более компактно решение (32) может быть записано в векторно- матричном виде:
. Более компактно решение (32) может быть записано в векторно- матричном виде: 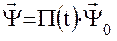 , где
, где 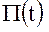 – матрица коэффициентов при компонентах вектора
– матрица коэффициентов при компонентах вектора 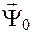 в системе уравнений (32). Матрицу
в системе уравнений (32). Матрицу 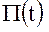 иногда называют матрицей прогноза, поскольку она осуществляет преобразование начального вектора состояния
иногда называют матрицей прогноза, поскольку она осуществляет преобразование начального вектора состояния 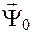 в вектор
в вектор 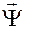 , соответствующий моменту
, соответствующий моменту 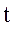 .
.
Если прогноз осуществляется на некоторый момент в будущем 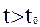 , аргумент
, аргумент 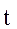 матрицы прогноза считают положительным, если прогноз осуществляется на момент в прошлом
матрицы прогноза считают положительным, если прогноз осуществляется на момент в прошлом 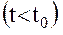 , аргумент
, аргумент 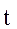 считается отрицательным, причем
считается отрицательным, причем 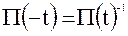 . Имеет место также следующее свойство матрицы прогноза: если
. Имеет место также следующее свойство матрицы прогноза: если 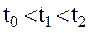 , то
, то
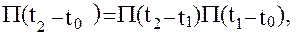
так как
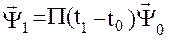
и
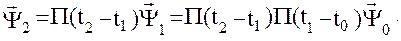
Этот вывод можно обобщить на несколько временных интервалов
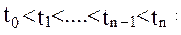
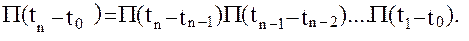
Важной особенностью решения (32) однородной системы дифференциальных уравнений (31) является независимость движения в плоскости опорной орбиты (компоненты 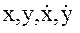 ) и уравнений, описывающих боковое движение в плоскости, перпендикулярной к плоскости опорной орбиты (компоненты
) и уравнений, описывающих боковое движение в плоскости, перпендикулярной к плоскости опорной орбиты (компоненты 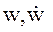 ). Пользуясь указанным свойством, рассмотрим геометрию движения двух близких искусственных спутников в плоскости опорной орбиты более подробно.
). Пользуясь указанным свойством, рассмотрим геометрию движения двух близких искусственных спутников в плоскости опорной орбиты более подробно.
Дата добавления: 2017-06-02; просмотров: 273;
