Двух искусственных спутников
Рассмотрим систему двух искусственных спутников 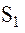 и
и 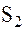 , в некоторый момент
, в некоторый момент 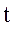 находящихся на расстоянии
находящихся на расстоянии 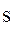 друг от друга в точках с координатами
друг от друга в точках с координатами 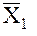 и
и 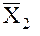 (см. рис. 1). Координаты спутников даны здесь в правой прямоугольной планетоцентрической экваториальной системе координат
(см. рис. 1). Координаты спутников даны здесь в правой прямоугольной планетоцентрической экваториальной системе координат 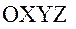 , которую далее будем называть абсолютной.
, которую далее будем называть абсолютной.
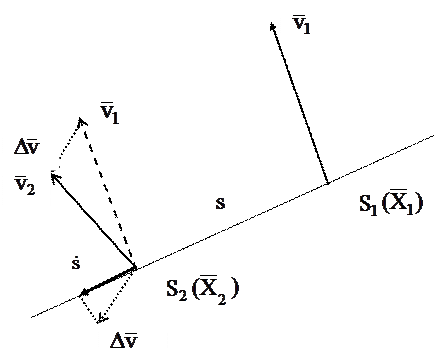
Рис.1.
Векторы линейных скоростей спутников 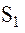 и
и 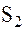 в абсолютной системе координат обозначим символами
в абсолютной системе координат обозначим символами 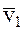 и
и 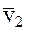 соответственно, символом
соответственно, символом 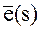 обозначим орт направления
обозначим орт направления 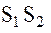 . Тогда относительная дальность между спутниками (скалярная величина):
. Тогда относительная дальность между спутниками (скалярная величина):
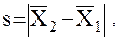 (6)
(6)
относительная скорость (вектор):
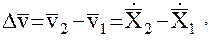 (7)
(7)
и относительное ускорение (вектор):
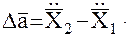 (8)
(8)
Спроектируем вектор 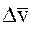 на направление
на направление 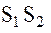 , получая значение относительной лучевой скорости
, получая значение относительной лучевой скорости 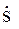 спутников в абсолютной системе координат:
спутников в абсолютной системе координат:
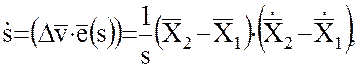 (9)
(9)
поскольку
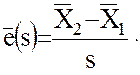
Изменение относительной лучевой скорости 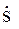 со временем получим путем дифференцирования равенства (9):
со временем получим путем дифференцирования равенства (9):
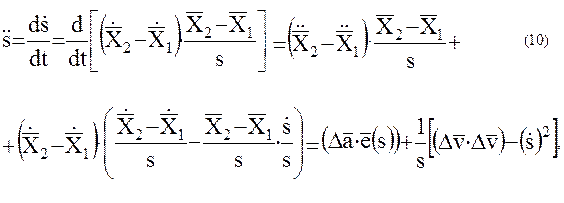
где 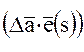 - проекция вектора относительного ускорения на луч зрения
- проекция вектора относительного ускорения на луч зрения 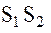 .
.
Предположим далее, что спутник 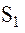 обращается по круговой орбите радиуса
обращается по круговой орбите радиуса 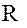 . Введем правую прямоугольную вращающуюся орбитальную спутникоцентрическую систему координат
. Введем правую прямоугольную вращающуюся орбитальную спутникоцентрическую систему координат 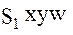 . Ось
. Ось 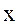 этой системы направим по вектору линейной скорости спутника
этой системы направим по вектору линейной скорости спутника 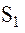 , ось
, ось 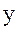 устремим по направлению его планетоцентрического радиуса-вектора, ось
устремим по направлению его планетоцентрического радиуса-вектора, ось 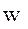 , дополняющая систему координат до правой тройки векторов, окажется при этом направленной по нормали к плоскости орбиты спутника
, дополняющая систему координат до правой тройки векторов, окажется при этом направленной по нормали к плоскости орбиты спутника 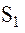 , часто называемой опорной орбитой.
, часто называемой опорной орбитой.
Будем полагать, что орбитальная система координат 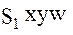 вращается в абсолютном пространстве с угловой скоростью
вращается в абсолютном пространстве с угловой скоростью 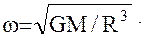 Тогда в системе координат
Тогда в системе координат 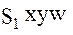 имеем для 1) вектора относительной дальности
имеем для 1) вектора относительной дальности 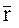 спутников
спутников 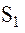 и
и 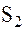 , 2) вектора относительной их скорости
, 2) вектора относительной их скорости 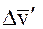 , 3) вектора относительного их ускорения
, 3) вектора относительного их ускорения 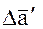 , 4) радиуса-вектора
, 4) радиуса-вектора 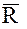 спутника
спутника 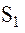 , 5) вектора угловой скорости вращения
, 5) вектора угловой скорости вращения 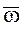 спутника
спутника 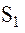 следующие представления в компонентах:
следующие представления в компонентах:
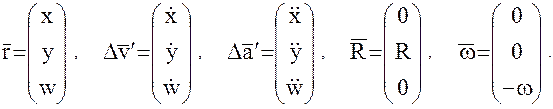
Зависимость между вектором скорости 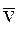 в абсолютной системе координат и вектором скорости
в абсолютной системе координат и вектором скорости 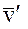 во вращающейся системе координат на основании теоремы Эйлера о распределении скоростей дается известным выражением:
во вращающейся системе координат на основании теоремы Эйлера о распределении скоростей дается известным выражением: 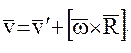 Для того, чтобы получить зависимость между относительными скоростями двух спутников в абсолютной и вращающейся системах координат предположим, что в момент
Для того, чтобы получить зависимость между относительными скоростями двух спутников в абсолютной и вращающейся системах координат предположим, что в момент 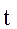 спутник
спутник 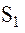 находится в точке с координатами
находится в точке с координатами 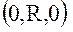 , а спутник
, а спутник 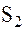 - в точке с координатами
- в точке с координатами 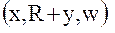 . Тогда вектора абсолютных скоростей спутников равны:
. Тогда вектора абсолютных скоростей спутников равны:
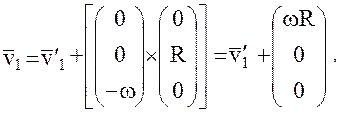
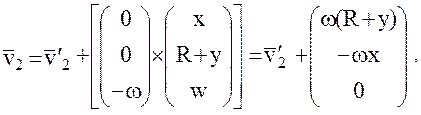
а искомый вектор относительной их скорости в абсолютной системе координат будет иметь вид:
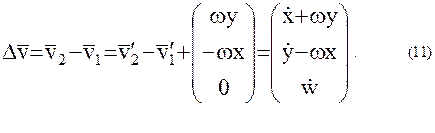
В согласии с (9) относительная лучевая скорость 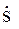 как проекция вектора относительной скорости
как проекция вектора относительной скорости 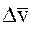 на направление
на направление  будет равна:
будет равна:
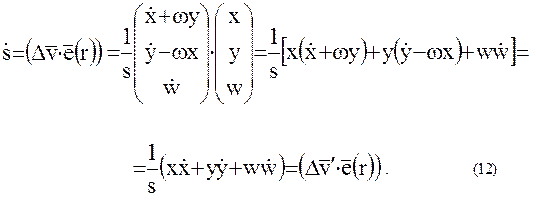
Равенство (12) означает, что значение относительной лучевой скорости двух искусственных спутников не зависит от того, измеряется ли она в абсолютной или во вращающейся системе координат.
Зависимость между относительными ускорениями в абсолютной 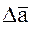 и вращающейся
и вращающейся 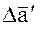 системах координат (при
системах координат (при 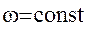 ) дается выражением:
) дается выражением:
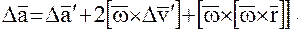 (13)
(13)
Выполняя в (13) операции векторного перемножения, получим для кориоллисова ускорения, возникающего в результате одновременного вращения системы координат и движения спутника относительно вращающейся системы:
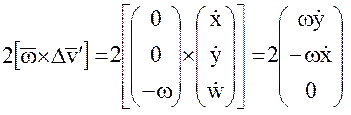
и переносного (центробежного) ускорения:
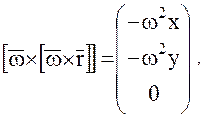
откуда имеем:
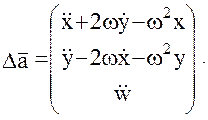 (14)
(14)
В заключение параграфа еще раз обратим внимание на то, что бортовые измерения характеристик относительного движения спутников выполняются во вращающейся орбитальной системе координат. Оценивание же по данным бортовых измерений значений параметров модели гравитационного потенциала требует преобразования измеряемых характеристик относительного движения в абсолютную планетоцентрическую систему координат.
1. Динамика относительного движения
искусственных спутников
Для получения уравнений наблюдений межспутниковых измерений необходимо определить вектора положений и скоростей, входящих в систему искусственных спутников, что может быть сделано в результате решения дифференциальных уравнений, описывающих их движение. Запишем эти уравнения в абсолютной планетоцентрической системе координат 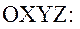
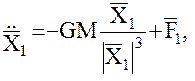 (15)
(15)
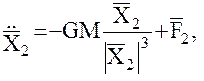 (16)
(16)
где 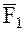 и
и 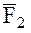 представляют собой векторные суммы ускорений, возмущающих движение спутников
представляют собой векторные суммы ускорений, возмущающих движение спутников 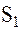 и
и 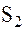 соответственно, относительно кеплеровского их движения в центральном гравитационном поле. Другими словами, при
соответственно, относительно кеплеровского их движения в центральном гравитационном поле. Другими словами, при 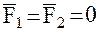 рассматриваемая задача сводится к задаче двух тел, решением которой является движение каждого из спутников по кеплеровскому эллипсу.
рассматриваемая задача сводится к задаче двух тел, решением которой является движение каждого из спутников по кеплеровскому эллипсу.
Образуем разность
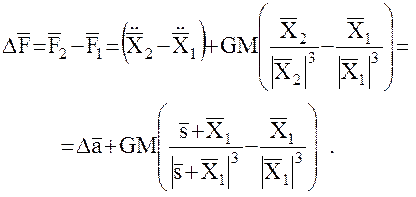
Учтем далее, что
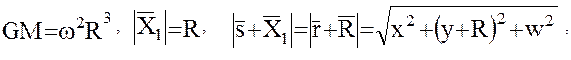
вследствие чего
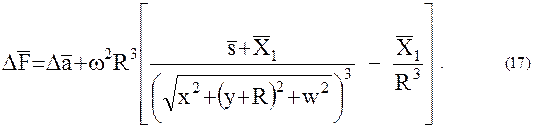
Переходя в орбитальную систему координат 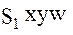 , подставим в (17) выражение (14) и получим дифференциальные уравнения относительного движения двух искусственных спутников в покомпонентной форме:
, подставим в (17) выражение (14) и получим дифференциальные уравнения относительного движения двух искусственных спутников в покомпонентной форме:
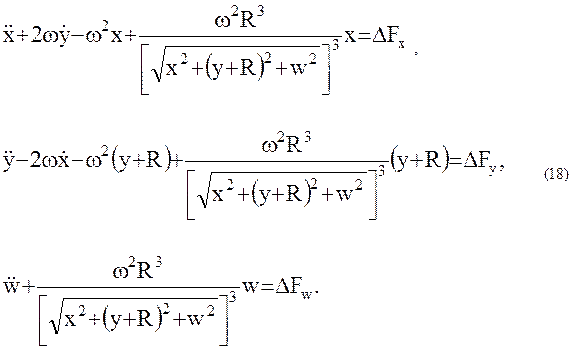
Уместно здесь будет подчеркнуть, что система дифференциальных уравнений второго порядка (18) представляет собой систему точных уравнений движения спутника 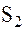 относительно спутника
относительно спутника 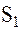 .
.
Компоненты 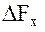 ,
, 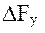 ,
, 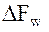 в общем случае являются нелинейными функциями координат и скоростей обоих искусственных спутников. Для решения уравнений такого рода, как правило, используются численные методы, которые в большинстве случаев оказываются единственно эффективным средством решения задач баллистического функционирования спутниковой системы.
в общем случае являются нелинейными функциями координат и скоростей обоих искусственных спутников. Для решения уравнений такого рода, как правило, используются численные методы, которые в большинстве случаев оказываются единственно эффективным средством решения задач баллистического функционирования спутниковой системы.
Дата добавления: 2017-06-02; просмотров: 306;
