Колебательная система автомобиля

Автомобиль представляет собой многомассовую колебательную систему, которая обладает многими степенями свободы. Как уже упоминалось ранее, массы всех частей автомобиля подразделяются на подрессоренные и неподрессоренные. Подрессоренные опираются на подвеску автомобиля (кузов, рама и закрепленные на них системы и механизмы), а неподрессоренные – на дорогу (мосты, колеса).

Подрессоренные массы колеблются на упругих устройствах подвески (рессоры, пружины, торсионы, пневмобаллоны и др.) с низкими частотами, составляющими 60–150 мин^-1, а неподрессоренные – на упругих устройствах подвески и шинах с высокими частотами – 350–700 мин^-1.

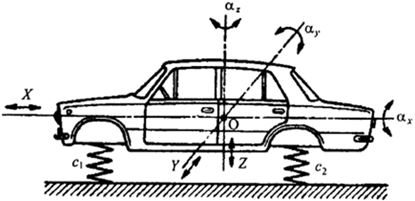
Кузов (рама) автомобиля при движении совершает сложное колебательное движение, перемещаясь поступательно (параллельно самому себе) вдоль трех взаимно перпендикулярных осей х, у, z и одновременно имея угловые перемещения относительно каждой из этих осей. При этом кузов может совершать шесть различных колебаний, соответствующих шести степеням свободы (рис. 12.1, а):

– поступательные вертикальные перемещения относительно вертикальной оси z (подпрыгивание);

– поступательные продольные перемещения относительно продольной оси х (подергивание);

– поступательно поперечные перемещения относительно поперечной оси у (шатание);

– угловые перемещения вокруг поперечной оси у (галопирование);

– угловые перемещения вокруг поперечной оси х (покачивание);

– угловые перемещения вокруг поперечной оси z (рыскание).

За начало координат принимают центр тяжести.

Главное влияние на плавность хода и на самочувствие человека в автомобиле оказывают два вида колебаний: поступательное вертикальное (подпрыгивание) и угловые продольные (галопирование).

а

б

а – автомобиля как колебательной системы; б – для определения приведенной

жесткости подвески

Рисунок 11.1 – Схема колебаний автомобиля

Колебания в вертикальной плоскости зависят от жесткости упругого элемента подвески и шин.

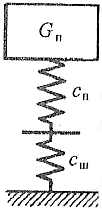
При определении приведенных жесткостей автомобиля с₁ и с₂ необходимо знать соответствующие жесткости подвесок и шин передней и задней осей. Для этого учитывают вес автомобиля, приходящийся на ось G₁ (G₂) жесткость подвески и шин соответственно C_п и С_ш (рис. 12.1, б).

Подбирая характеристику упругого элемента к конкретной модели автомобиля, добиваются искомой плавности хода в вертикальной плоскости.

Дня смягчения вертикальных колебаний желательно иметь мягкую подвеску, которая значительно деформируется при переезде препятствия, а для гашения нежелательных медленно затухающих колебаний кузова использовать амортизаторы.

Более сложное влияние на плавность хода оказывает галопирование. Если возмущающая сила Р приложена не к центру упругости, а в другой точке, то возникает как линейное, так и угловое перемещение (рис. 12.2).

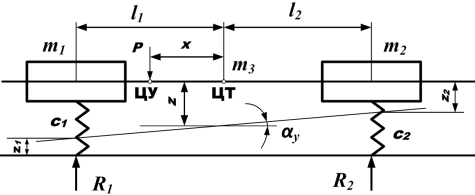
Рисунок 12.2 – Модель колебаний автомобиля

Из условия равновесия системы относительно центра тяжести:

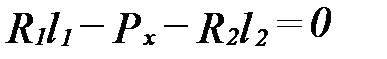
(12.4)

где R₁ и R₂ – реакции опор;

х – расстояние от центра упругости до ЦТ, .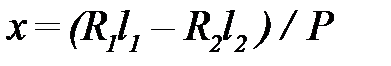

Учитывая, что реакции опор R₁ и R₂ можно выразить через жесткость и деформации упругих элементов, получим: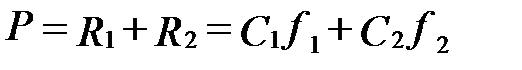

Подставив в выражение для определения расстояния (х) найденные значения R₁, R₂ и Р, получим:

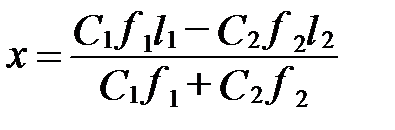
(12.5)

Если сила Р приложена к центру упругости, то происходит только линейное перемещение. В этом случае f₁ = f₂ и галопирование отсутствует, а выражение (12.5) примет вид:

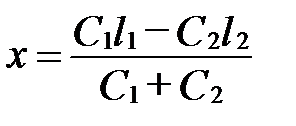
(12.6)

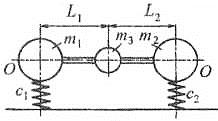
Полученное выражение можно применить к колебаниям кузова, заменив подрессоренную массу т_п тремя массами – т₁, m₂ и т₃, связанными между собой невесомым стержнем (рис. 12.3, а). Массы т₁ и т₂ расположены соответственно на расстояниях l₁ и l₂ от центра тяжести кузова, а масса т₃ находится непосредственно в центре тяжести.

а

б

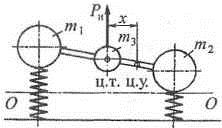
а – колебательная система эквивалентная подрессоренной массе;

б – положение центра тяжести и упругости

Рисунок 12.3 – Схема для расчета колебаний автомобиля

Чтобы система из этих трех тел была подобна подрессоренной массе автомобиля, должны выполняться следующие условия:

– сумма всех масс системы должна быть равна подрессоренной массе автомобиля: т₁ + m₂ + т₃ = т_п;

– центр тяжести системы должен совпадать с центром тяжести подрессоренной массы, т.е. m₁l₁ = т₂l₂;

– момент инерции системы относительно горизонтальной оси (у)должен быть равен моменту инерции подрессоренной массы относительно той же оси: m₁l²₁+ m₂l²₂ = т_к ρ²_к, где ρ_к – радиус инерции подрессоренной массы автомобиля.

В соответствии с перечисленными условиями определим массы:

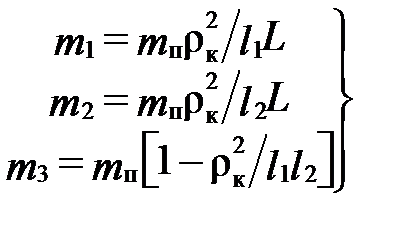
(12.7)

Если вывести систему из состояния равновесия, а затем отпустить, то возникнут колебания (рис. 12.3, б), при которых появится сила инерции Р_и, равная произведению массы m₃ на ускорение колебаний, которая создает момент относительно центра упругости: М_и = Р_и·х. Момент инерции во время колебаний будет равен нулю при условии, если m₃ = 0 или плечо силы инерции х = 0.

Из системы (12.7) следует, что (m ₃ = 0), если (ρ²_к / (l₁l₂) = 1), т.к. (т_п ≠ 0). Для легковых автомобилей отношение ρ²_к /(l₁l₂) близко к 1, поэтому они имеют достаточно хорошую плавность хода.

Если центр плеча (х = 0) и центр тяжести совпадает с центром упругости системы, то х = (C₁l₁ – C₂l₂) / (С₁ + С₂) = 0 и С₁/С₂ = l₂ / l₁.

Следовательно, жесткость подвесок необходимо выбирать таким образом,чтобы они были обратно пропорциональны расстояниям центpa тяжести от передней и задней осей. Тогда при одинаковых прогибахподвесок кузов будет перемещаться вертикально без галопирования.