Работа и мощность тока. Закон Джоуля-Ленца

Кулоновские и сторонние силы при перемещении заряда q вдоль электрической цепи совершают работу A. Рассмотрим однородный проводник с сопротивлением R, к концам которого приложено напряжение U. Если по проводнику течет ток I, то за время dt через сечение проводника переносится заряд dq=Idt. Тогда работа электростатических сил по перемещению заряда q между точками цепи 1 и 2 равна:

.

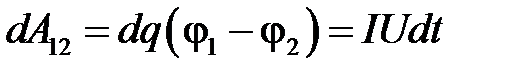Мощность, развиваемая на участке цепи между точками 1 и 2, равна (исходя из определения мощности):

.

Работа, совершаемая током, приводит к выделению энергии. Например, если ток протекает по обмоткам электродвигателя, то это механическая энергия; если заряжается аккумулятор – химическая; работа тока также переходит в тепловую энергию (нагревая проводник и окружающее его пространство).

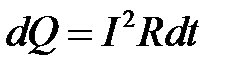
и мощности P:

.

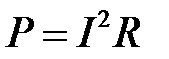Выражение называют законом Джоуля-Ленца.

Закон Джоуля-Ленца (в интегральной форме): количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.

Напомним, что единицей измерения количества теплоты и работы в системе СИ является джоуль (Дж), а мощности – ватт (Вт). В технике часто используют внесистемные единицы работы тока: ватт·час (Вт·ч) и киловатт·час (кВт·ч). 1 Вт·ч – это работа электрического тока мощностью 1 Вт в течение 1 ч. Таким образом, 1 Вт·ч=3,6·10³ Вт·с =3,6·10³ Дж (так как Вт·с=Дж); аналогично: 1 кВт·ч=1000 Вт·ч=3,6·10⁶ Дж. Отметим, что бытовые приборы учета потребленной электроэнергии определяют работу, совершенную электрическим током. В технике также используется внесистемная единица количества теплоты – калория (1 кал = 4,1868 Дж).

Аналогично тому, как выводится закон Ома в дифференциальной форме, выводится закон Джоуля-Ленца в дифференциальной форме – закон, определяющий количество теплоты, выделяющееся в единичном объеме проводника в единицу времени – удельную тепловую мощность тока w:

.

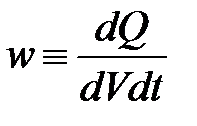Рассмотрим однородный цилиндрический проводник:

,

где S – площадь поперечного сечения проводника, l – его длина, а V=Sl – объем проводника.

Мощность, выделяемая в единице объема проводника, – удельная тепловая мощность тока, равна:

.

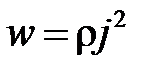Эквивалентные выражения закона Джоуля-Ленца в дифференциальной форме:

.

Для количества теплоты dQ, выделяющегося в объеме dV за время dt:

.

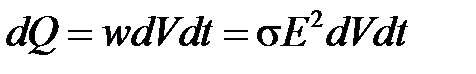В случае неоднородного проводника можно найти количество тепла, выделяемого в каждой точке объема неоднородного проводника.