Первое уравнение Максвелла

Уравнения Максвелла

Краткая история

Формулировке уравнений Максвелла предшествовали открытия законов взаимодействий заряженных тел, намагниченных тел и проводников с электрическим током. При этом были сформулированы закон Кулона, закон Ампера, закон Био Савара – Лапласа.

В 1831 M. Фарадей открыл явление электромагнитной индукции и сформулировал закон, описывающий это явление. Кроме того, примерно в то же время он ввёл понятие электрического и магнитного поля как самостоятельных физических субстанций.

Опираясь на представление Фарадея о поле, и введя ток смещения, равнозначный по своему магнитному действию обычному электрическому току, Дж. К. Максвелл сформулировал систему уравнений, названную впоследствии уравнениями Максвелла.

Уравнения Максвелла функционально связывают электрическое и магнитное поле с зарядами и токами и охватывают собой все известные закономерности электромагнетизма. Первоначально Максвелл прибегал к вспомогательным механическим моделям "эфира", но уже в "Трактате об электричестве и магнетизме" (1873) электромагнитное поле рассматривалось как самостоятельный физический объект.

Физической основой уравнений Максвелла является принцип близкодействия, утверждающий, что передача электромагнитных возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Этот принцип противоположен классическому ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние .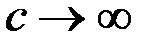

Математическим аппаратом теории Максвелла является векторный анализ. Максвелл считал, что его заслуга состоит лишь в математическом оформлении идей Фарадея.

Каноническая форма

Каноническая форма записи, принятая ныне, принадлежит Г. Герцу и О. Хевисайду и основана на использовании векторных полей: напряжённости электрического поля 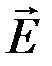, напряжённости магнитного поля 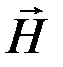, векторов электрической индукции 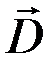и магнитной индукции .

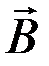Уравнения Максвелла связывают эти величины между собой, а также с плотностью электрического заряда 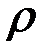и плотностью электрического тока , которые рассматриваются как источники электрического и магнитного поля соответственно.

Первое уравнение Максвелла

В 1820 году датский физик Эрстед демонстрировал электрический ток и обнаружил, что вокруг проводника с током существует магнитное поле. Это было обнаружено по действию электрического тока на магнитные стрелки, расположенные около проводника с током. Экспериментально с помощью железных опилок или набора магнитных стрелок было установлено, что магнитные линии являются замкнутыми. Тогда можно говорить, что магнитное поле имеет вихревой характер. Математически это записывается с помощью оператора «ротор», этот оператор записывается символами или . Характеристикой магнитного поля является его напряженность 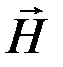, поэтому говорят о вихрях напряженности магнитного поля. Они существуют не только вокруг тока проводимости, но и вокруг тока смещения. Тогда этот экспериментальный факт можно записать с помощью уравнения:

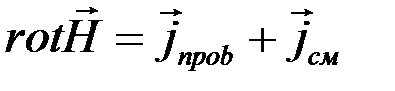(2.1)

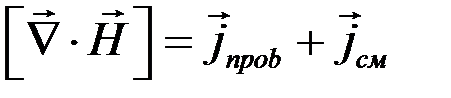(2.1.1)

Здесь 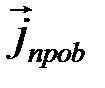- плотность тока проводимости, а 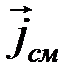- плотность тока смещения.

Формула (2.1) представляет собой первое уравнение Максвелла в дифференциальной форме. При интерпретации этого уравнения необходимо понимать следующее:

1. Уравнение (2.1) утверждает, что вокруг любого тока существует вихревое магнитное поле;

2. Выражение «электрический ток порождает магнитное поле» не совсем корректно для постоянного тока, так как не существует системы отсчета, в которой проводник с током существовал бы отдельно от магнитного поля;

3. Нельзя говорить, что постоянный ток порождает постоянное магнитное поле, так как они существуют в единстве, и здесь нет причинно-следственной связи;

4. В случае переменных полей можно говорить, что изменяющееся электрическое поле порождает магнитное поле. Но об этом речь в другом уравнении Максвелла;

5. Уравнение (2.1) является описанием бесконечно малой окрестности некоторой изучаемой точки.

Получим первое уравнение Максвелла в интегральной форме. Для этого умножим скалярно формулу (2.1) на вектор 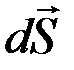и проинтегрируем по поверхности всей площадки:

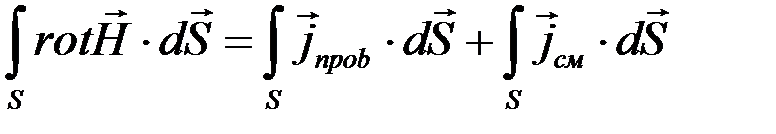(2.2)

Применим к левой части уравнения (2.2) формулу Стокса:

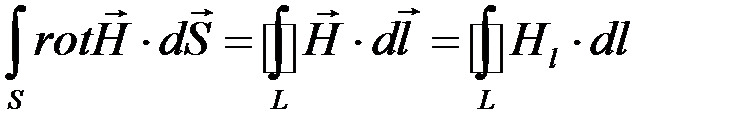(2.3)

Здесь 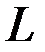- замкнутый контур, ограничивающий поверхность 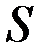, а 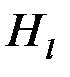- проекция вектора напряженности магнитного поля на касательную к контуру. Подставляем формулу (2.3) в формулу (2.2):

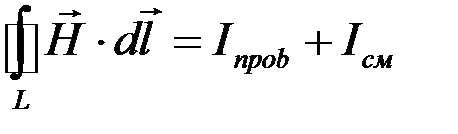(2.4)

Здесь по определению плотности тока записаны значения тока проводимости и тока смещения:

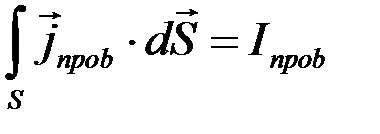(2.5)

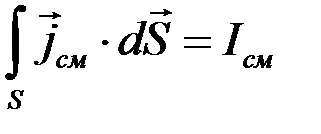(2.6)

Уравнение (2.4) представляет собой первое уравнение Максвелла в интегральной форме. Оно имеет тот же смысл, что и уравнение в дифференциальной форме, только здесь речь идет о конечном замкнутом контуре и конечной площадке.

Физическая сущность первого уравнения Максвелла в интегральной форме – вокруг тока проводимости и тока смещения существуют вихри магнитного поля.