Система уравнений (2).

Полученная система уравнений (2) носит название системы уравнений Шеннона симметричной формы записи. Основу системы дифференциальных уравнений Шеннона составляет интеграл Стилтьеса:

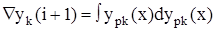, (3)

где 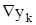(i+1)-это приращение интеграла вычисляемой функции на (i+1) шаге:

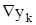(i+1)=y_k(i+1) - y_ki (4)

Для вычисления интеграла (3) в цифровых интеграторах реализуются частные формулы численного интегрирования:

1.Частные формулы численного интегрирования нулевого порядка (или первого порядка точности). Они называются формулами Эйлера1 и Эйлера2.

Формула прямоугольника с недостатком:

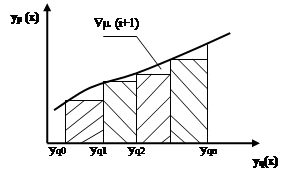
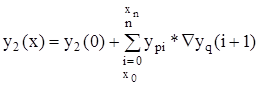
Ñm - приращение методической ошибки.

Ñm(i+1)= 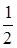hy_p(x)

Ñm(i+1) – погрешность метода на одном шаге интегрирования.

h – шаг интегрирования.

y_p – некоторое значение (промежуточное) подинтегральной функции на шаге интегрирования.

Погрешность вычисления зависит от шага.

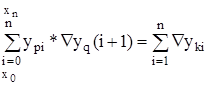- это приращение интеграла по шагам.

Формула прямоугольника с избытком.

.

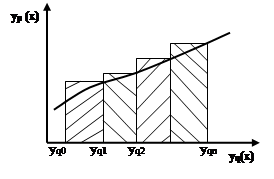
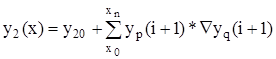Формула трапеций.

Ñm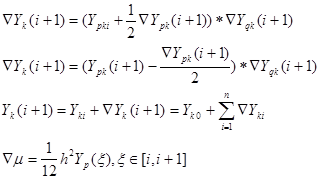
-погрешность.

Заменой в системе дифференциальных уравнений Шеннона дифференциалов разностями и численными формулами интегрирования получаются разностные схемы систем уравнений Д.У. Шеннона, которые являются алгоритмами работы цифровых интеграторов.