Система уравнений (1).
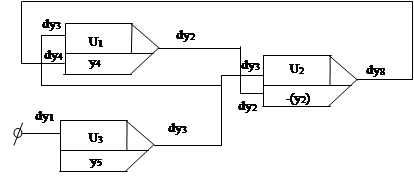Структурная схема вычислителя функции y=sin wt.
у4(0)= max
у2(0)= 0
у2(0)= y20
у4(0)= y40
у5(0)= w=const
Рис.1.
Достоинства: простота, высокая скорость вычисления (за один такт работы цифрового интегратора получаем значение вычисляемой функции). Кроме функии у2 вычисляется одновременно и множество других функций на этом же шаге: одновременно получается значение cos wt – это переменная у4, и значение аргумента wt – это у3.Поэтому в задаче не требуетмся производить дополнительных вычислений для получения этих значений.
Система уравнений (1) может решаться параллельно рисунку 1, когда весь процесс происходит одновременно на трёх интеграторах; и может решаться последовательно используя только один интегратор, а все промежуточные данные хранятся в ЗУ.
Вычислительное устройство должно содержать три функциональных блока:
1. цифровой интегратор;
2. сумматор приращения;
3. экстрополятор (Э) приращения.
dy2=y4*dy3; y4*- это значение, при последовательной обработке, нужно проэкстрополировать.
dyk=ypkdyqk
dyk – дифференциал вычисляемой функции.
ypk- подитегральная переменная для к-той функции.
dyqk- дифференциал переменной интегрирования q к-той функции.
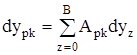
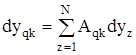
k=2,3,…,N , где N- последняя вычисляемая переменная.
p=0,1,2,…,N,N+1,…,B ,где N+1,…,B- определяют номера констант, которые входят в подинтегральную функцию.
q=1,2,3,…,N – дифференциал.
ypk(0)= ypk0 (начальное условие).
Дата добавления: 2017-04-20; просмотров: 264;