Разностная схема систем дифференциальных уравнений Шеннона.

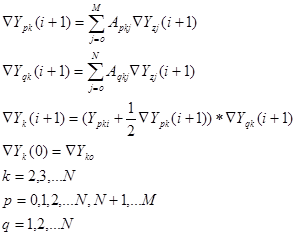
Источники погрешностей работы систем дифференциальных уравнений Шеннона.

1. Инструментальная погрешность, определяется точностью представления данных в разрядной сетке системы. Рассчитывается разрядность переменных и приращений (как в обычных ЦВМ).

2. Методическая погрешность, определяется методической погрешностью частных формул численного интегрирования. (Например, формула трапеций более точная, чем формула прямоугольников.)

3. А) Погрешность квантования, образуется за счет отбрасывания младших разрядов при вычислении до числа n, определенного при расчете инструментальной погрешности. Это погрешность квантования первого рода.

Б) Погрешность квантования второго рода, образуется за счет того, что в вычислениях участвуют уже квантованные величины.

Для борьбы с погрешностью квантования используют метод округления с учетом отбрасываемого разряда. В этом случае величина погрешности не превышает единицы младшего разряда, не зависимо от интервала интегрирования.

4. Трансформированная погрешность, которая возникает от неточного задания входных

данных. Она определяется коэффициентом передачи решаемой задачи. Способ сокращения трансформированная погрешности: выравнивание значений масштабных коэффициентов в решаемой задаче за счет изменения размерности физических и математических переменных.

СУШ позволяет решать задачу на последовательной ЦИС (цифровая интегрирующая система) и параллельной ЦИС. Каждый ЦИ (цифровой интегратор) реализует одну из частных формул численного интегрирования. ÑY_k(i+1), ÑYp_k(i+1) - квантованные величины.

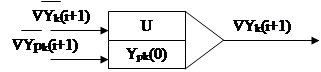Структурная схема цифрового интегратора.

Х – умножитель,

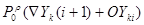Реализует функцию расчленения .

В исходном состоянии регистр остатка равен нулю. Для реализации ЦИ существуют специальные серии элементов: К502. Появление инструментальных средств таких как: Альтерра, Xilinx, позволяют реализовать не отдельные интеграторы, а специализированные интегрирующие системы на одной БИС.