Нетрадиционного типа.
Проблемно – ориентированные процессоры – это процессоры, система команд которого и структура ориентированы на решение задач определённого класса: инженерных, экономических, управления, моделирования и т. д. Процессоры имеют универсальную систему команд то есть способны решить любую задачу, но технические характеристики в этом случае будут хуже, чем при решении задач на которые он ориентирован.
Рассмотрим один из вариантов проблемно – ориентированного процессора, который называется цифровая – интегрирующая машина. Это машина, которая в системе команд имеет всего три команды:
1.Численного интегрирования по Стилтьесу (базовая операция).
2.Операция суммирования приращений.
3.Экстраполяция приращений.
Шеннон показал, что любую математическую зависимость можно представить в виде системы дифференциальных уравнений (ДУ) и эта система называется системой дифференциальных уравнений Шеннона (СУШ). Методы перехода от произвольной математической зависимости к ДУ : исходная математическая зависимость дифференцируется и вводятся подстановки до тех пор, пока промежуточная функция не начнёт повторяться или обратится в ноль.
| ФУНКЦИЯ | ПОДСТАНОВКА | СУШ |
| Сложение - вычитание. у2= y3+y4 у2= y3-y4 | dу2=dy3+dy4 dу2= dy3-dy4 | |
| Умножение. у2= y3*y4 dу2= y3dy4+ y4dy3 | dу5= y3dy4 dу6= ydy | dу2=dy5+dy6 dу6= y3dy4 dy5=y4dy3 |
Деление.
у2= 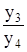 =y3* =y3* 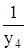 =
=y3*y5 =
=y3*y5
| у5= 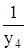 ;
dу5= - ;
dу5= - 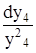 = - = - 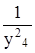 dy4= - y8 dy4;
y8=y25 dy4= - y8 dy4;
y8=y25
| dу2=dy6+dy7; dу6= y3dy5; dy7=y5dy3; dу5= - y8dy4; dу8=2 y5dy5=y9dy5; dy9=2dy5 |
Структурная схема блока, выполняющего операцию деления.
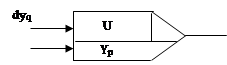
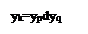
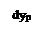
Основу составляет интегратор.
S-сумматор.


 Достоинство: операция выполняется за один такт.
Достоинство: операция выполняется за один такт.
| ФУНКЦИЯ | ПОДСТАНОВКА | СУШ |
| у= sin wt у2=sin y3 | y2=y; y1=t; y3=wt; y4=cosy3; y5=w | dу2=cosy3dy3; dу4= - siny3dy3; dу3= wdy1; |
w-круговая частота, t-входной аргумент.
Отсюда СУШ будет:
dу2=cosy3dy3
dу4= - y2dy3
dу3= y5dy1
Начальные условия:
у2(0)= y20
у4(0)= y40
у5(0)= w=const
 dу1=t
dу1=t
Дата добавления: 2017-04-20; просмотров: 410;
