Ранговый коэффициент корреляции

В тех случаях, когда основные статистические характеристики в генеральной совокупности, из которой формируется выборка, оказываются за пределами параметров нормального или близкого к нему закона распределения, можно рекомендовать применение ранговой корреляции. С этой целью используют прежде всего ранжирование статистической совокупности отдельно по вариантам факторного и результативного признаков. Далее расчет рангового коэффициента корреляции проводится по формуле:

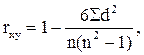(11.4)

где r _xy – коэффициент ранговой корреляции между признаком-фактором и признаком-результатом; d – разность между ранговыми номерами вариант по признаку-фактору и признаку-результату; n – численность выборки.

Определение коэффициента ранговой корреляции покажем на примере, отражающем взаимосвязь между урожайностью и трудоемкостью льносоломки в 50 сельскохозяйственных организациях (табл. 11.4).

Т а б л и ц а 11. 4. Расчет вспомогательных показателей для определения рангового коэффициента корреляции

№ п.п.	х, ц/га	у, чел.-ч/ц	№ по х	№ по у	d	d²
					-49
					-47
					-45
					-43
					-41
…	…	…	…	…	…	…

Σ	-	-	-	-	-

Теперь подставим необходимые данные в формулу 11.4; получим:

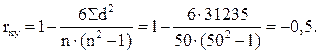
Рассчитанный коэффициент корреляции (r _xy = – 0,5) указывает на наличие обратной зависимости между урожайностью и трудоемкостью льносоломки, причем тесноту связи между этими признаками можно оценить как среднюю.

Теснота (сила) зависимости результативных признаков от факторных повышается по мере приближения к единице. Условно принято считать, что если корреляционное отношение или коэффициент корреляции не превышает 0,3, то зависимость можно признать слабой, от 0,3 до 0,7 – средней, свыше 0,7 – тесной.

<68 69 707172 73 74 >

Дата добавления: 2017-04-20; просмотров: 245;