Коэффициенты прямолинейной парной корреляции
Если взаимосвязь между изучаемой парой признаков выражается в форме, близкой к прямолинейной, то степень тесноты связи между этими признаками можно рассчитать при помощи коэффициента прямолинейной парной корреляции. В настоящее время имеется много различных способов расчета коэффициента парной корреляции. Каждый способ учитывает характер и особенности взаимосвязей между изучаемыми признаками в статистической совокупности. Доказано, что наиболее точный результат корреляционной тесноты связи между факторным и результативным признаками может быть получен по формуле
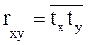 , (11.2)
, (11.2)
где r ху – коэффициент парной корреляции между признаком-фактором (х) и признаком-результатом (у); tx – нормированное отклонение по признаку-фактору; t y – нормированное отклонение по признаку-результату.
Коэффициенты корреляции, также как и корреляционные отношения, обладают стабильным свойством, заключающимся в том, что пределы колебаний этих показателей могут быть выражены следующим образом: -1< r ху < 1. Это означает, что коэффициенты корреляции и корреляционные отношения могут колебаться в пределах, не превышающих единицу.
Сокращенный вариант расчета коэффициента парной корреляции между урожайностью сена многолетних трав и годовым удоем коров в 100 сельскохозяйственных организациях по формуле 11.3 приведен в табл. 11.1.
Т а б л и ц а 11. 1. Расчет вспомогательных показателей для определения коэффициента парной корреляции
| № п.п. | х, ц/га | 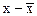 ,
ц/га ,
ц/га
| 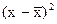
| 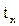 ,
ц/га ,
ц/га
| у, ц | 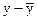 ,
ц ,
ц
| 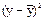
| 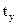 ,
ц ,
ц
| 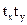
|
| -10 | -1,0 | -15 | -1,5 | 1,5 | |||||
| -9 | -0,9 | -15 | -1,5 | 1,4 | |||||
| -8 | -0,8 | -1,0 | 0,8 | ||||||
| ... | … | .. | … | … | … | … | … | … | … |
| 2,0 | 1,5 | 3,0 | |||||||
| Σ | - | - | - | - | 70,0 | ||||
| Среднее | - | 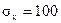
| - | - | 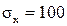
| - | 0,7 |
Как видно, полученное среднее произведение нормированных отклонений по признаку-фактору и признаку-результату 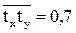 представляет собой коэффициент парной корреляции между этими признаками. Поскольку этот коэффициент положительный, то взаимосвязь между признаками прямая, а величина коэффициента корреляции (r = 0,7) указывает на среднюю меру зависимости годового удоя одной коровы от урожайности сена многолетних трав.
представляет собой коэффициент парной корреляции между этими признаками. Поскольку этот коэффициент положительный, то взаимосвязь между признаками прямая, а величина коэффициента корреляции (r = 0,7) указывает на среднюю меру зависимости годового удоя одной коровы от урожайности сена многолетних трав.
Необходимо иметь в виду, что абсолютная величина коэффициента корреляции, как и корреляционного отношения, может колебаться от 0 до 1, а с учетом направления связи – находиться в пределах от – 1 до 1. При этом чем ближе коэффициент корреляции к единице (отрицательной или положительной), тем теснее находятся признаки во взаимосвязи.
Расчет коэффициента корреляции по основной формуле 11.2 хотя и дает довольно точный результат, но отличается повышенной трудоемкостью вычисления. Поэтому для измерения степени тесноты связи между факторным и результативным признаками можно рекомендовать формулу, предложенную К. Пирсоном:
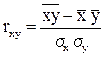 , (11.3)
, (11.3)
где r xy – коэффициент прямолинейной парной корреляции; 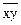 – среднее произведение факторного и результативного признаков:
– среднее произведение факторного и результативного признаков: 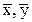 – среднее значение соответственного факторного и результативного признаков,
– среднее значение соответственного факторного и результативного признаков, 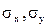 –– средние квадратические отклонения признака-фактора и признака-результата.
–– средние квадратические отклонения признака-фактора и признака-результата.
При расчете коэффициента прямолинейной парной корреляции по формуле 11.3 в общем виде можно воспользоваться макетом вспомогательной табл. 11.2.
Т а б л и ц а 11.2. Схема расчета вспомогательных показателей
Дата добавления: 2017-04-20; просмотров: 513;
