Интерпретация уравнения регрессии

Проанализируем, какую информацию дает нам оцененное уравнение регрессии (2.6), т.е. поставим вопрос об интерпретации (содержательном объяснении) коэффициентов уравнения.

Во-первых, можно сказать, что увеличение X на одну единицу (в единицах измерения переменной X) приведет к увеличению/уменьшению (в зависимости от знака коэффициента 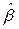) значения Y на 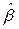единиц (в единицах измерения переменной Y).

Во-вторых, необходимо проверить, в каких единицах измерены переменные X и Y и можно ли заменить слово "единица" фактическим количеством (рубли, тонны и т.п.).

В-третьих, константа 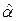дает прогнозируемое значение Y, если положить X=0. Это может иметь или не иметь экономического смысла в зависимости от конкретной ситуации.

Часто рассчитывают средний коэффициент эластичности 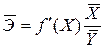, который показывает, на сколько процентов в среднем по совокупности изменится результат Y от своей средней величины при изменении фактора X на 1% от своего среднего значения.

Пример. Продолжая рассмотрение примера п. 2.1, проинтерпретируем уравнение регрессии между индивидуальным потреблением и личными доходами в США: 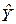=-2,91+0,9276X.

Поскольку обе переменные измерены в $, то интерпретация облегчается.

Смысл коэффициента 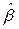: при увеличении личных доходов граждан США на 1$ расходы на индивидуальное потребление возрастут на 0,9$. Другими словами, из каждого дополнительного доллара дохода 90 центов будут израсходованы на потребление.

Константа в данном случае не имеет никакого смысла применительно к совокупности, поскольку мы не можем сказать, что при нулевых доходах потребление граждан США составит -2,91 млрд. долларов.

Рассчитаем средний коэффициент эластичности:

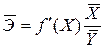=0,9276×350/351,75=0,923.

Т.е. при изменении личных доходов на 1% от своего среднего значения в среднем по совокупности индивидуальное потребление изменится на 0,923% от своей средней величины. Ñ

При интерпретации уравнения регрессии важно помнить о следующих фактах:

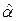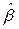§ величины и являются только оценками a и b, а следовательно, и вся интерпретация представляет собой тоже оценку;

§ уравнение регрессии отражает общую тенденцию для выборки, а каждое отдельное наблюдение при этом подвержено воздействию случайностей;

§ верность интерпретации зависит от правильности спецификации уравнения, то есть включения/исключения соответствующих объясняющих переменных и выбора вида функции регрессии.