Количественный и стоимостной подход

Графический подход

Расчет маржи безопасности (запаса финансовой прочности) и операционного рычага

4. Допущения анализа «затраты – объем – прибыль»

Литература:

1. Воронова Е.Ю. Управленческий учет : учебник для бакалавров / Е.Ю. Воронова. – М.: Издательство Юрайт, 2012. – 551с. – С. 282-318

2. Друри К. Управленческий учет для бизнес-решений : учебник / Пер. с англ. – М.: ЮНИТИ-ДАНА, 2012, - 655с. – С.61-85

В хозяйственной деятельности предприятия часто возникают следующие вопросы: Сколько единиц продукции следует продать, чтобы выйти на уровень безубыточности? Какое воздействие на прибыль оказало бы снижение цены реализации или реализация большего количества продукции? Какой требуется объем реализации для покрытия дополнительных постоянных издержек в связи с проведением рекламной компании? На эти и другие вопросы может помочь ответить метод «Затраты – объем - прибыль» или CVP – анализ (cost – volume – profit).

Количественный и стоимостной подход

Цель CVP - анализа состоит в том, чтобы установить, что произойдет с финансовыми результатами при изменении уровня производственной деятельности (деловой активности) организации.

CVP – анализ основан на зависимости между доходами от продаж, издержками и прибылью в течение краткосрочного периода.

Под краткосрочным периодом понимается промежуток времени (обычно год или меньше) в течение которого выход продукции предприятия ограничен уровнем имеющихся в настоящее время в его распоряжении действующих производственных мощностей. Большинство затрат и цены на продукцию предприятия определяются заранее, и основной областью неопределенности является объем реализации.

Существуют три основных подхода к анализу затраты – объем – прибыль:

Количественный,

Стоимостной;

Графический.

При количественном подходе объем продаж выражается в количестве проданных единиц продукции, при стоимостном – величиной полученной выручки. В основе графического способа лежит графическая интерпретация постоянных и переменных затрат, величины совокупной выручки и совокупных издержек.

Введем следующие условные обозначения:

Ц – цена за единицу продукции;

V – количество проданных единиц продукции;

И_пер – совокупные переменные затраты;

S _пер – средние переменные затраты на единицу продукции;

И _пост - совокупные постоянные затраты;

Пр – прибыль до налогообложения.

МД_уд – маржинальный доход на единицу продукции

В результате получим:

Ц 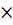V - выручка от реализации продукции

S_пер 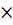V -совокупные переменные затраты.

Тогда прибыль до налогообложения определится выражением:

Пр = Ц 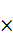V - S_пер 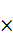V – И _пост (1)

Для ответа на вопрос, сколько единиц продукции должно быть продано для того, чтобы получить требуемую величину прибыли, преобразуем уравнение (1):

Пр = (Ц - S _пер) 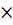V – И _пост(2)

Откуда:

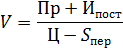
(3)

Разница между ценой и средними переменными затратами на единицу продукции и есть маржинальный доход на единицу продукции:

МД_уд = 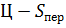(4)

Таким образом, при количественном подходе к анализу соотношения «затраты – объем - прибыль» формула для определения количества продукции, обеспечивающего необходимую величину прибыли, имеет вид:

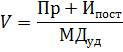
(5)

Одним из направлений анализа соотношения «затраты – объем - прибыль» является определение точки безубыточности, т.е. объема выпуска, который обеспечит безубыточную деятельность.

Используя выражение (1), можно найти такой объем продаж (в единицах продукции), при котором совокупные доходы предприятия равняются совокупным затратам:

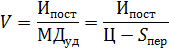
(6)

Количественный подход к анализу соотношения «затраты – объем - прибыль» позволяет ответить и на ряд вопросов, связанных с исчислением целевой прибыли.

Первый вопрос - сколько единиц продукции необходимо продать, чтобы получить определенную прибыль до налогообложения ? Для ответа на этот вопрос подставляем сумму целевой прибыли до налогообложения в формулу (5):

Второй вопрос - сколько единиц продукции должно быть реализовано для того, чтобы получить прибыль до налогообложения в размере, например, 20% выручки?

Выручка от продаж выражается как Ц 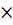V. Тогда воспользовавшись уравнением 2 получим:

Пр = (Ц - S _пер) 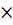V – И _пост

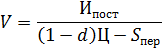
где 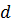- удельный вес прибыли до налогообложения в размере выручки.

Третий вопрос - какое количество единиц продукции необходимо реализовать для того, чтобы обеспечить определенный размер чистой прибыли, при условии, что ставка налога на прибыль составляет n %?

Допустим, что β_нп – ставка налога на прибыль, тогда налог на прибыль составит:

НП = Пр 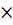β_нп,

а чистая прибыль будет равна:

Прч = Пр(1 – β_нп).

Соответственно, прибыль до налогообложения будет равна:

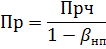
Данную формулу необходимо подставить в выражение 3 и решить его.