Простейшие теоремы статики
Теорема о переносе силы вдоль линии действия: Действие силы на твердое тело не изменится от переноса
Теорема о трех силах: если твердое тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таких трех сил пересекаются в одной точке. Обратная теорема неверна, т.е. если линии действия трех сил пересекаются в одной точке, то такая система сил не обязательно является равновесной.
Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке – центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.
Таким образом, система 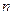 сходящихся сил эквивалентна одной силе
сходящихся сил эквивалентна одной силе 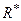 , которая и является равнодействующей этой системы сил.
, которая и является равнодействующей этой системы сил.
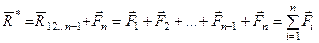 . (9)
. (9)
Проецируя векторы векторного равенства на прямоугольные оси координат, получим:
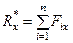 ;
; 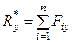 ;
; 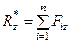 . (10)
. (10)
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам
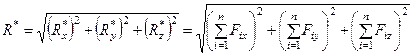 ;(11)
;(11)
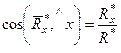 ,
, 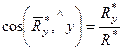 ,
, 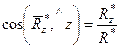 ; (12)
; (12)
Теорема о моменте равнодействующей силы (теорема Вариньона): векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки:
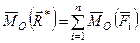 . (13)
. (13)
Теорема Вариньона относительно оси 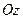 : момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
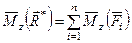 , (14)
, (14)
Для случая плоской системы сил, если точку 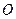 выбрать в плоскости действия сил, получаем теорему Вариньона для плоской системы сил: алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.
выбрать в плоскости действия сил, получаем теорему Вариньона для плоской системы сил: алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.
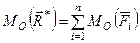 . (15)
. (15)
Дата добавления: 2017-01-29; просмотров: 744;
