Вопрос 2. Особенности оценки стоимости долевых и долговых ценных бумаг
В основе оценки лежит базовая модель, однако особенности той или иной ценной бумаги вносят в нее коррективы.
- Стоимость облигаций с нулевым купоном.
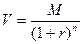
M – сумма, выплачиваемая при погашении облигации (номинал); r – требуемая инвестором ставка доходности; n – количество лет до срока погашения.
2. Стоимость безотзывных (не допускающих досрочного погашения) облигаций с постоянным доходом.
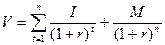
I – ежегодный купонный доход.
Если проценты по облигациям уплачиваются несколько раз в год, то формула трансформируется. Например, если проценты выплачиваются раз в полугодие, то
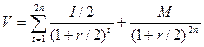 .
.
3. Стоимость отзывных облигаций с постоянным доходом. Отзывная облигация отличается от безотзывной наличием двух дополнительных характеристик: выкупной цены (Pc) и срока защиты от досрочного погашения (m). Если инвестор полагает, что вероятность досрочного погашения мала, то расчет производится по предыдущей формуле. Если с точки зрения инвестора вероятность досрочного погашения велика, в расчетах вместо М используется цена отзыва, а прогнозный интервал равен сроку защиты от погашения:
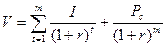 .
.
4. Стоимость акций с неравными по годам дивидендами определяется по формуле базовой модели стоимости финансового актива.
5. Стоимость акций с постоянным дивидендом и неопределенно долгим периодом владения (в основном – привилегированные акции):
V = D / r
D – ежегодный дивиденд.
6. Стоимость акций с равномерно возрастающими дивидендами оценивается с использованием модели Майрона Гордона:
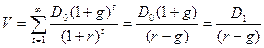 ,
,
g – темп прироста дивидендов; D0 – последний выплаченный дивиденд; D1 – первый ожидаемый дивиденд (дивиденд в первом прогнозном периоде).
Трансформация формулы основана на том, что она представляет собой сумму членов бесконечной геометрической прогрессии, в которой первый член 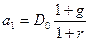 , а знаменатель прогрессии
, а знаменатель прогрессии 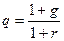 . Сумму бесконечной убывающей геометрической прогрессии можно рассчитать по формуле:
. Сумму бесконечной убывающей геометрической прогрессии можно рассчитать по формуле: 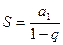 . Подставляя в эту формулу выражения для первого члена и знаменателя прогрессии, получаем модель Гордона.
. Подставляя в эту формулу выражения для первого члена и знаменателя прогрессии, получаем модель Гордона.
(Рассматриваемая прогрессия является убывающей, так как принимается допущение r>g, в противном случае модель Гордона не имеет смысла).
7. Стоимость акций с изменяющимся темпом прироста дивидендов определяется путем разбиения интервала прогнозирования на подпериоды, каждый из которых характеризуется собственным темпом прироста. Например, если выделено два подпериода с темпами прироста g и p, то формула имеет вид:
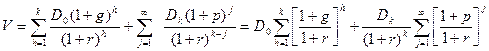
Возможна трансформация формулы. Первое слагаемое представляет собой сумму k членов убывающей геометрической прогрессии, где первый член 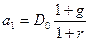 и знаменатель прогрессии
и знаменатель прогрессии 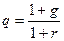 . Сумму k членов убывающей прогрессии можно рассчитать по формуле:
. Сумму k членов убывающей прогрессии можно рассчитать по формуле: 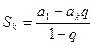 . Подставляя в эту формулу выражения для первого члена и знаменателя, получим первое слагаемое. Второе слагаемое соответствует модели Гордона, то есть сумме бесконечно убывающей геометрической прогрессии, где первый член
. Подставляя в эту формулу выражения для первого члена и знаменателя, получим первое слагаемое. Второе слагаемое соответствует модели Гордона, то есть сумме бесконечно убывающей геометрической прогрессии, где первый член 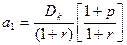 и знаменатель
и знаменатель 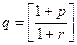 . Таким образом, получим
. Таким образом, получим
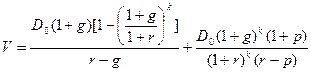 .
.
Дата добавления: 2017-01-29; просмотров: 499;
