Способы начисления процентов

Существует два принципиально разных способа начисления процентов: декурсивный и антисипативный.

При декурсивном способе проценты начисляются в конце каждого интервала начисления, исходя из суммы капитала, предоставленного на начало временного интервала. Декурсивная процентная ставка (i) называется ссудным процентом и определяется по формуле:

i = I / PV,

где I – процентный доход за определенный временной интервал; PV – сумма денег на начало временного интервала.

При антисипативном способе начисления процентов они начисляются в начале каждого интервала начисления, исходя из наращенной суммы денег на конец интервала (включающей капитал и проценты). Антисипативная процентная ставка (d) называется учетной ставкой и определяется по формуле:

d = I / FV,

где I – процентный доход за определенный временной интервал; FV – наращенная сумма денег на конец временного интервала.

На практике наибольшее распространение получил декурсивный способ начисления процентов. Антисипативный способ применяется в операциях учета векселей и других денежных обязательств. Сумма денег на конец интервала начисления считается величиной получаемого кредита. Так как проценты начисляются в начале временного интервала, то заемщик получает сумму кредита за вычетом процентов. Такая операция называется дисконтированием по учетной ставке или банковским учетом. Дисконт – это разница между размером кредита и непосредственно выдаваемой суммой, то есть доход, полученный банком по учетной ставке.

Как при декурсивном, так и при антисипативном способах могут использоваться схемы начисления простых и сложных процентов. При использовании схемы простых процентов они начисляются на сумму первоначального вклада. Сложный процент предполагает капитализацию процентов, то есть начисление «процентов на проценты».

С точки зрения кредитора, при проведении финансовых операций краткосрочного характера (менее года) более выгодна схема простых процентов, а при долгосрочных операциях (более года) – схема сложных процентов. При долгосрочных операциях с дробным числом лет выгодна так называемая смешанная схема, когда в течение целого числа лет начисляются сложные проценты, а в течение дробной части года – простые проценты.

В табл. систематизированы формулы определения наращенной суммы денег, то есть будущей стоимости вклада, при декурсивном и антисипативном способах начисления процентов. При этом использованы следующие обозначения:

FV – будущая (наращенная) сумма денег;

PV – настоящая (текущая) сумма денег;

i – ставка ссудного процента;

d – учетная ставка;

n – число лет в интервале начисления процентов;

m – число внутригодовых начислений процентов;

t – продолжительность интервала начисления процентов при краткосрочных операциях, дней;

T – продолжительность года, дней;

w – целое число лет в интервале начисления;

f – дробная часть года в интервале начисления.

Таблица

Формулы расчета наращенной суммы денег при различных условиях начисления процентов

Условия начисления процентов	Способ начисления процентов
Декурсивный	Антисипативный
простой процент, целое число лет в интервале начисления	FV = PV´ (1 + in)	FV = PV / (1 – dn)
сложный процент, целое число лет в интервале начисления	FV = PV´ (1 + i)n	FV = PV / (1 – d)n
простой процент, срок операции менее года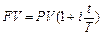
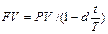
смешанная схема начисления процентов при дробном числе лет в интервале начисления	FV = PV´ (1 + i)w (1 + if)	FV = PV / [(1 – d)w (1 + if)]
сложный процент, внутригодовые начисления с целым числом лет в интервале начисления процентов	FV = PV´(1 +i/m)nm	FV = PV / (1 –d/m)nm