Этап VI. Получение оптимального решения или переход к новому циклу.
Будем в новой, полученной на этапе V таблице, содержащей числа Cij(2), искать оптимальное решение, как это описывалось в этапе II. Если мы при этом придем к оптимальному решению, то процесс заканчивается. В противном случае мы повторим этапы III, IV и V и, в случае необходимости, вернемся к этапу II еще раз. Полученное в результате описанных действий оптимальное решение может оказаться неединственным. Продолжим операции в нашем примере. Повторив этап II, мы получаем таблицу 6.9, которая будет содержать новые перечеркнутые или обведенные нули. Приступим к этапу III; пометим строку 5, а потом столбец 3; после этого мы должны пометить строку 1, а следовательно, и столбец 4, на основании чего появляется пометка против строки 2.
Таблица 6.9
  1 1
| 12,5 | 6,5 | |||
 2 2
| 11,5 | 8,5 | |||
 3 3
| 7,5 | 7,5 | |||
  4 4
| 5,5 | 12,5 | 7,5 | ||
 5 5
| 8,5 | 1,5 |
Прочеркнем строки 3 и 4 и столбцы 3 и 4; это составит этап IV. Перейдем к этапу V: наименьшее число свободной части табл. 6.10, которая только что была нами получена, есть 1,5. Вычтем его из элементов столбцов 1, 2 и 5 и затем прибавим к элементам строк 3 и 4. В результате мы получим табл. 6.11.
На этот раз новое применение операций этапа II дает целиком нулевое решение:
C41(2) + C52(2) + C13(2) + C24(2) + C35(2) = 0
которое и является искомым. В первоначальной таблице этому решению соответствует
С41 + С52 + С13 + С24 + С35 = 4,5 + 9,5 + 9 + 5 + 5,5 = 33,5 часа.
Таблица 6.10
| 12,5 | 6,5 |   0 0
|  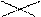 0 0
| x | ||
| 11,5 | 8,5 |  0 0
| x | |||
 7,5 7,5
| 7,5 |  0 0
| ||||
  0 0
| 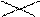 0 0
| 5,5 | 12,5 | 7,5 | ||
| 8,5 | 1,5 | 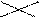 0 0
| x | |||
| x | x |
Таблица 6.11
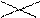  1 1
| 4,5 | ||||
 2 2
| 3,5 | ||||
 3 3
| 7,5 | 7,5 | 7,5 | 7,5 | |
  4 4
| 7,5 | ||||
 5 5
| 0 
| 10,5 |
Таблица 6.12
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Решение может быть, наконец, представлено, как и в таблице 6.2, в виде единиц и нулей, причем единицы будут занимать использованные клетки (табл. 6.12).
Таким образом, решение, которое приводит к минимальному суммарному времени ожидания в 33,5 часа, оказывается следующим:
1-я бригада живет в Мехико. Рейсы d и 1. Перерыв 4,5 часа.
2-я бригада живет в Акапулько. Рейсы 2 и е. Перерыв 9,5 часа.
3-я бригада живет в Акапулько. Рейсы 3 и а. Перерыв 9 часов.
4-я бригада живет в Мехико. Рейсы b и 4. Перерыв 5 часов.
5-я бригада живет в Акапулько. Рейсы 5 и с. Перерыв 5,5 часа.
Аналогичный расчет позволяет определить максимальное время простоя, которое составляет 83,5 часа. Между наилучшим и наихудшим решениями имеется разница в 50 часов и существует еще 118 промежуточных решений (не обязательно отличающихся друг от друга по существу; так, например, решения 2а, b1, 5с, d4, е3 и 2а, b1, 5с, d3, e4 эквивалентны друг другу). Кто теперь осмелится утверждать, что для нахождения оптимального решения достаточно интуиции и общих рассуждений, особенно если в таблице было бы еще несколько строк и столбцов?
3.3.3. Создание математической модели «Задачи о назначениях»
Рассмотренный выше алгоритм кажется не слишком сложным. Рассмотрим как его можно реализовать в ППММ.
Первое и главное, не забываем описать задачу, пусть кратко. См. рис. 3.25. На этом этапе также выбирается формат ввода исходных данных модели.
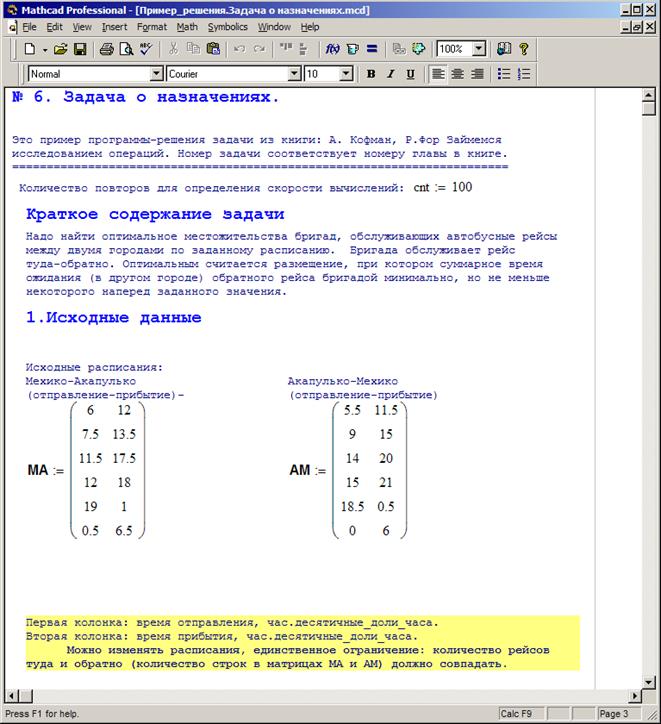
Рис. 3.25. Описание задачи и исходные данные.
Далее, приступаем к реализации алгоритма. В этом процессе следует придерживаться тактики «мелких прыжков в нужном направлении», т.е.:
1) не пытаться написать «сразу все»;
2) разбить алгоритм на мелкие, относительно независимые кусочки-действия;
3) реализовать каждое такое действие;
4) проверить корректность реализации каждого действия на тестовых данных (полная проверка корректности — очень сложная задача, но надо хотя бы убедится, что ваша программулька считает);
5) объединить действия в последовательность алгоритма;
6) сформировать и вывести результаты.
После того, как алгоритм создан из «мелких кусочков» и при необходимости, например, улучшить быстродействие, некоторые кусочки можно будет объединить. Если же скорость вычислений удовлетворительная, то лучше оставить «мелкие кусочки», ибо хорошо структурированные вычисления облегчают как последующие модификации алгоритма, так и понимание программы другими людьми.
Итак, первый «кусочек» алгоритма. В нашем случае алгоритм уже содержит хорошо структурированные «шаги», поэтому простейшим вариантом является последовательная реализация каждого из шагов. Первым шагом алгоритма является вычисление ожиданий при обслуживании рейсов бригадами живущими в первом из городов. Легко сообразить, что второй шаг алгоритма — вычисление ожиданий при обслуживании рейсов бригадами живущими во втором городе — в точности аналогичен первому. Ибо кто пронумеровал города? Поэтому есть резон написать универсальную программу для обеих случаев, см. рис. 3.26.
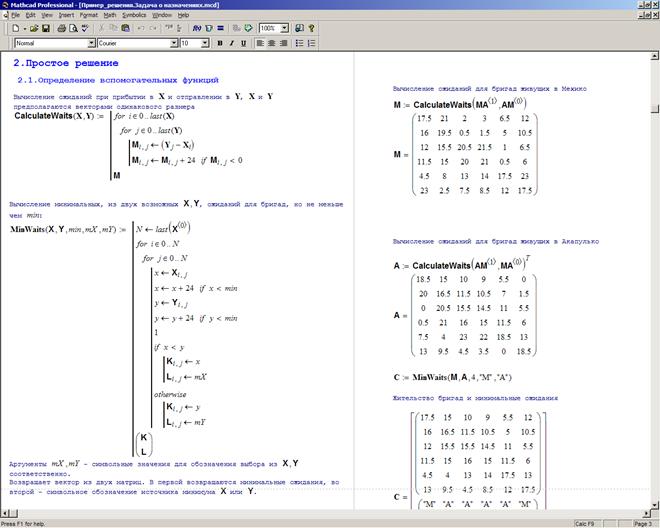
Рис. 3.26. Реализация первых шагов алгоритма.
На рис. 3.26 следует обратить внимание на КОММЕНТАРИИ к каждой из функций и тестовые расчеты (справа) для проверки работоспособности функции и демонстрации формата возвращаемых данных.
Реализация Этапа 1 алгоритма очень проста (рис. 3.27), но не следует отклоняться от «генеральной линии» — каждый этап реализуем отдельной функцией.
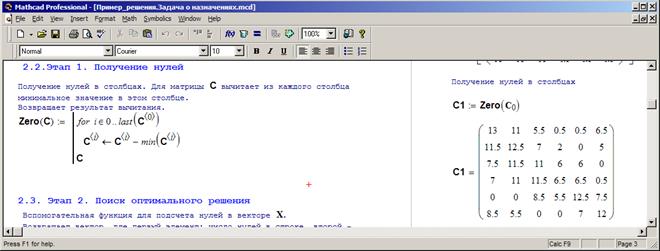
Рис. 3.27. Реализация Этапа 1 алгоритма.
Реализация Этапа 2 алгоритма — первый этап циклической части — заметно сложнее и может быть выражена в нескольких функциях, выполняющих элементарные действия. (рис. 3.28), но не следует отклоняться от «генеральной линии» — каждый этап реализуем отдельной функцией.
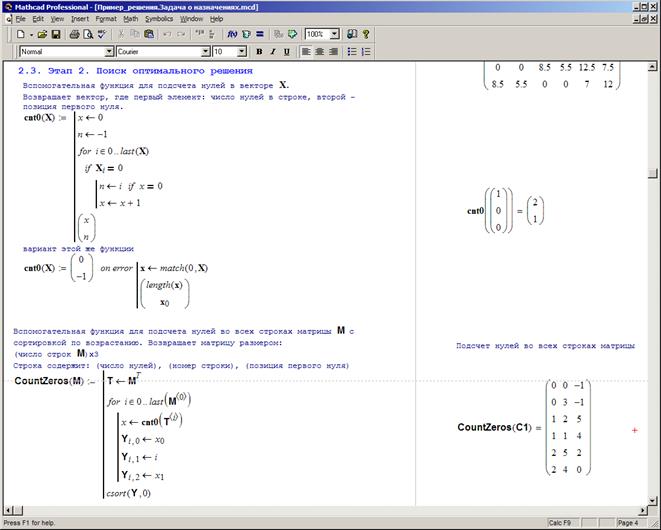
Рис. 3.28a. Реализация Этапа 2 алгоритма.
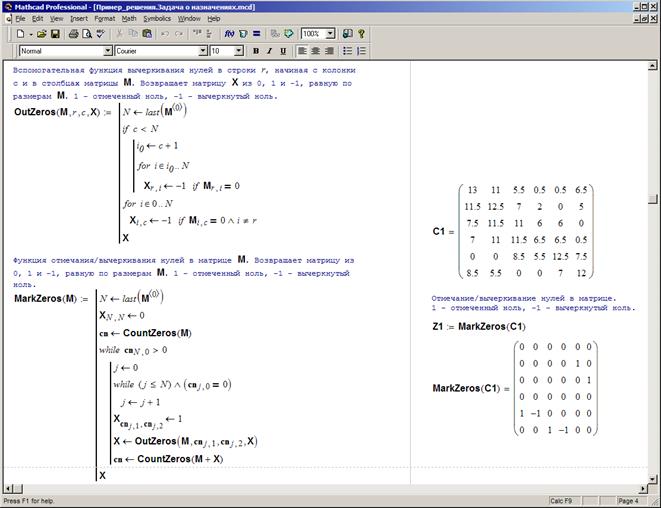
Рис. 3.28б. Реализация Этапа 2 алгоритма.
Этап 2 алгоритма достаточно сложен, чтобы использовать аж три вспомогательных функции, чтобы реализовать пометку и вычеркивание нулей в матрице.
Реализация Этапа 3 — самый сложный участок алгоритма. На этом этапе циклически повторяются сложные процедуры пометки строк и столбцов. При создании прикладной математической модели, по крайней мере на первоначальном этапе, следует каждую из процедур пометки реализовать отдельной функцией, см. рис. 3.29.
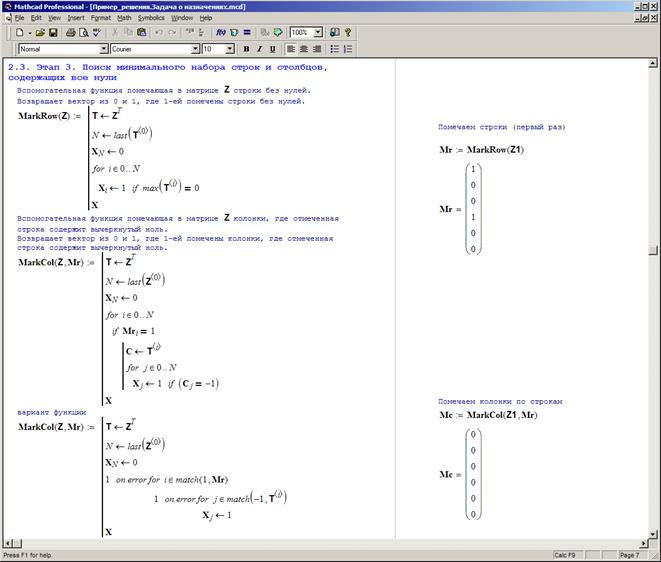
Рис. 3.29а. Реализация Этапа 3 алгоритма. Вспомогательные функции.
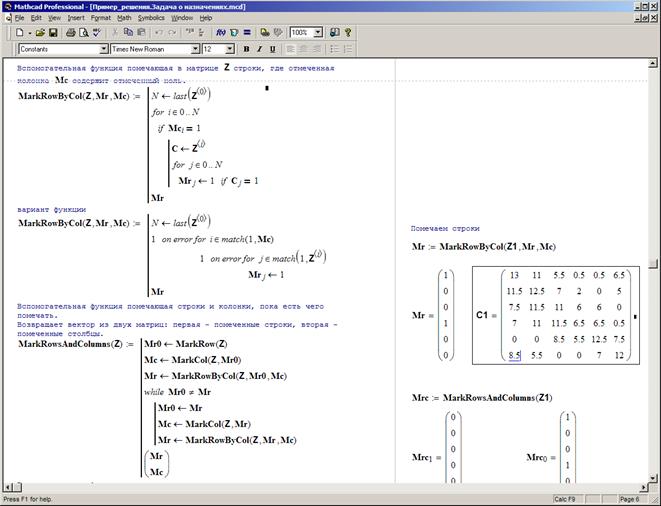
Рис. 3.29б. Реализация Этапа 3 алгоритма. Вспомогательные функции.
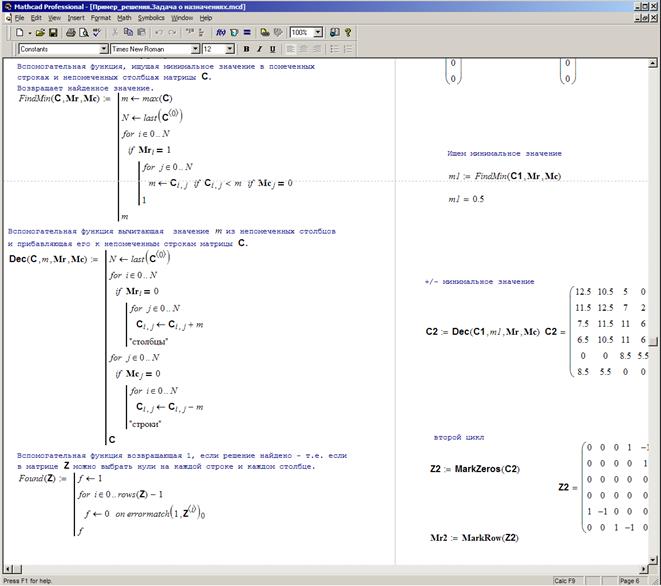
Рис. 3.29в. Реализация Этапа 3 алгоритма. Вспомогательные функции.
После того, как все вспомогательные функции определены, можно сконструировать основное тело алгоритма, см. рис. 3.30. В реализации математической модели следует обратить внимание на два момента:
1) ограничение числа итераций — чтобы при ошибках не возникало зависание;
2) возможность журналирования промежуточных шагов вычислений — для отладки алгоритма.
2.4. Основная функция определения решения.
Возвращает суперматрицу из 3-х элементов:
1) матрица из 4-х столбцов:
номер рейса туда,
номер рейса обратно,
город местожительства/отправления,
время ожидания между рейсами.
2) количество итераций затраченное на поиск.
3) Если параметр 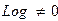 , то возвращаются данные всех промежуточных итераций. , то возвращаются данные всех промежуточных итераций.
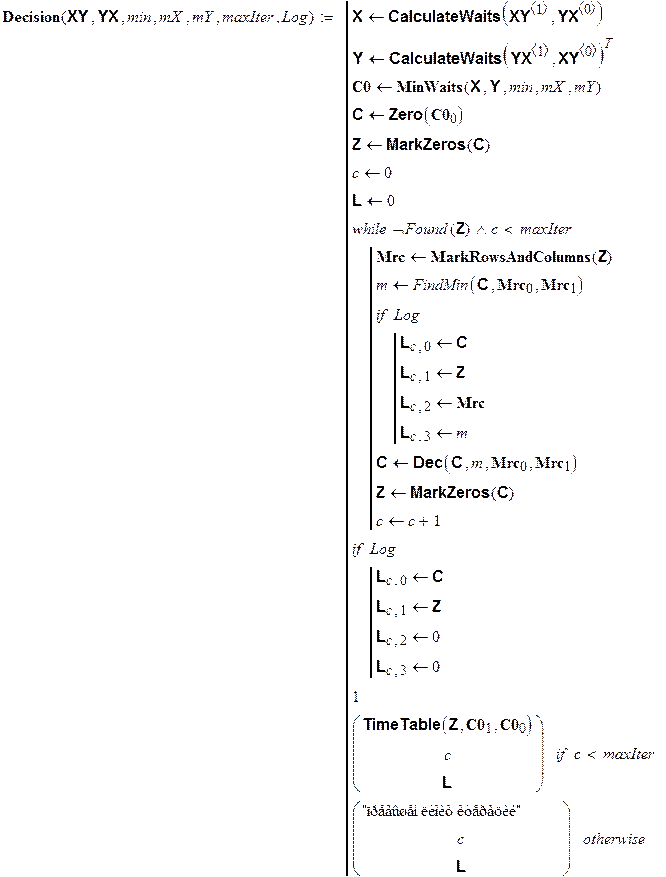
|
Рис. 3.30. Реализация алгоритма.
Ну и окончательно, следует позаботиться об описании результатов моделирования, см. рис. 3.31.
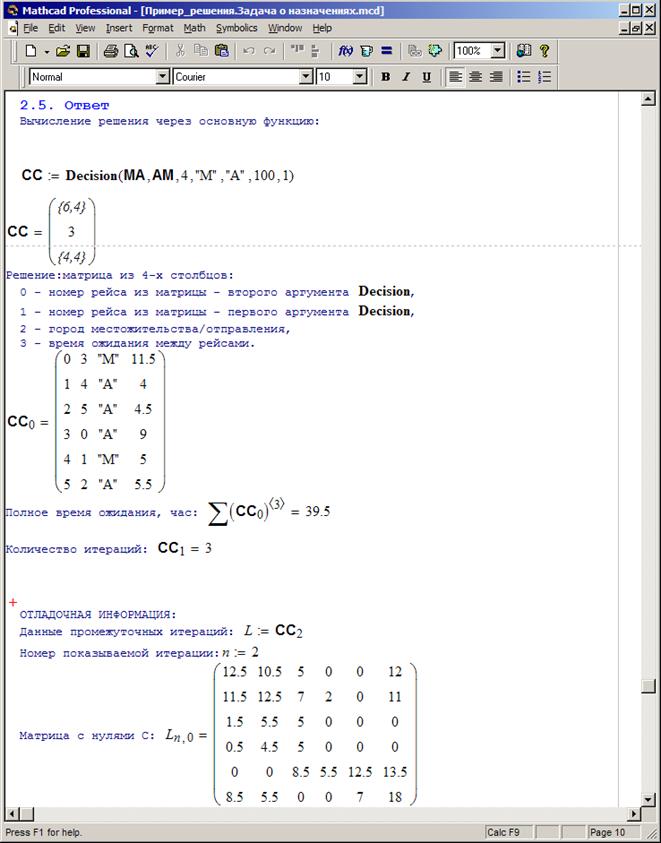
Рис. 3.31. Вывод результатов моделирования.
AnSYS
Общие сведения
Пакет прикладного математического моделирования ANSYS — типичный представитель специализированных пакетов математического моделирования. В сущности, ANSYS является объединением нескольких пакетов моделирования из различных разделов инженерных и физических расчетов, объединенных единым интерфейсом и возможностью обмена данными/результатами расчетов.
Основные АНАЛИТИЧЕСКИЕ модули ANSYS (12.0)
· Electric (ANSYS);
· Explicit Dynamics (ANSYS);
· Fluid Flow (CFX);
· Fluid Flow (Fluent);
· Harmonic Response (ANSYS);
· Linear Buckling (ANSYS);
· Magnetostatic (ANSYS);
· Modal (ANSYS);
· Random Vibration (ANSYS);
· Response Spectrum (ANSYS);
· Shape Optimization (ANSYS);
· Static Structural (ANSYS);
· Steady-State Thermal (ANSYS);
· Thermal-Electric (ANSYS);
· Transient Structural (ANSYS);
· Transient Structural (MBD);
· Transient Thermal (ANSYS);
· и т.д.
Набор модулей может расширяться, т.к. ANSYS — суть коллекция СПЕЦИАЛИЗИРОВАННЫХ прикладных пакетов моделирования. Кроме аналитических (т.е. расчетных) модулей, ANSYS содержит компоненты, предназначенные для подготовки расчетных моделей — генераторы сеток, графические редакторы и т.п.
В ранних версиях ANSYS эта коллекция была кучей отдельных программ. В современной версии ANSYS 12.0 пакеты объединены общим графическим интерфейсом ANSYS Workbench.
ANSYS Workbench — это оболочка над коллекцией разнородных модулей. Основанная на концепции «schematic view», это оболочка сводит воедино весь процесс моделирования и помогает пользователю пройти через сложный анализ разных физических процессов с помощью технологии «drag-and-drop». С помощью двусторонней связи и автоматизированного механизма обновления проекта оболочка обеспечивает управление и интеграцию всех возможностей ANSYS в технологии «Simulation Driven Product Development» (разработка на основе моделирования).
Графический интерфейс ANSYS Workbench Geometry Interfaces обеспечивает взаимосвязь с большинством основных модулей ANSYS (не со всеми!) и делает возможным принятие решений на основе моделирования. С помощью простых автогенерируемых сеток, которые можно тщательно доработать вручную ANSYS Meshing ускоряет процесс моделирования и помогает добиться более точного решения. ANSYS DesignModeler заполняет пропасть между данными CAD и моделированием, ANSYS DesignModeler обеспечивает создание специфических геометрических моделей для обеспечения задач анализа. ANSYS DesignXplorer дает возможность планирования эксперимента, оптимизацию, поиск экстремума и Six Sigma analysis (набор технологий для практического проектирования или разработки, улучшающий процессы производства и исключающий дефекты).
«Multiphysics»-моделирование ANSYS дает дружественные средства инженерного моделирования и анализа сложных связанных физических явлений. ANSYS «multiphysics» совмещает высокотехнологичные средства решения для всех физических разделов: структурной механики, теплопереноса, течения сплошной среды и электромагнетизма.
Модуль ANSYS «Structural Mechanics» предлагает лучшие средства моделирования для разработки продукции, минимизирующие необходимость физического прототипирования и уменьшающие время проектирования. Этот модуль охватывает широкий спектр задач по анализу типов, элементов, контактов, материалов, решателей уравнений, направленных на понимание и решение сложных проблем проектирования.
Модуль ANSYS «Fluid Flow» предлагает весьма полный набор инструментов для решения задач механики жидкости и газа и сопутствующих проблем. Возможности «Fluid Flow» обеспечивают все необходимое для проектирования новых устройств и анализа уже существующих. Модуль содержит как расчетные подсистемы общего назначения, так и специализированные системы для промышленных расчетов.
Модуль ANSYS «Explicit Dynamics» предназначен для моделирования больших деформаций, растяжений, разрывов и др. случаев разрушения материалов.
Модуль ANSYS «Electromagnetics» обеспечивает моделирование электромагнитных полей. Позволяет инженерам точно предсказывать поведение электрических и электромеханических устройств.
Все модули описывать мы не будем.
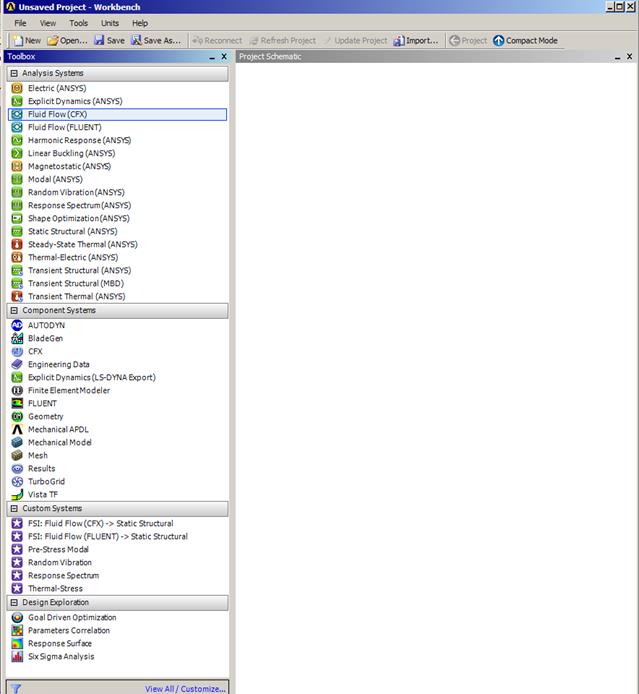
Рис. 3.32. Окно ANSYS Workbench.
Дата добавления: 2017-01-13; просмотров: 1185;
