Применение MathCAD для построения моделей
Лучше один раз увидеть, чем сто раз услышать. Разберем использование MathCAD на примере построения несложной модели. Естественно, мы предполагаем, что нам известна вся теория, которую надо знать для построения модели.
В качестве примера для построения модели возьмем задачу оптимизации расписания. Для этой задачи известно решение, но нас это не должно смущать, ибо наша цель — попрактиковаться в построении математической модели средствами MathCAD.
Итак, задача!
3.3.1. Постановка «Задачи о назначениях»
Рейс Мехико — Акапулько обслуживают роскошные автобусы компании «Золотой Пеликан», а также автобусы конкурирующих компаний. Обслуживающая автобус бригада состоит из шофера и кондукторши. Вот расписание движения по маршруту Мехико — Акапулько и Акапулько — Мехико:
| Мехико – Акапулько | |||
| Отправление из Мехико | Номер рейса | Прибытие в Акапулько | |
| 06:00 |  a a
| 12:00 | Время в пути 6 часов |
| 07:30 |  b b
| 13:30 | |
| 11:30 |  c c
| 17:30 | |
| 19:00 |  d d
| 01:00 | |
| 00:30 | 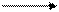 e e
| 06:30 |
| Акапулько – Мехико | |||
| Прибытие в Мехико | Номер рейса | Отправление из Акапулько | |
| 11:30 | 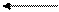 1 1
| 05:30 | Время в пути 6 часов |
| 15:00 |  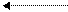 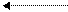 2 2
| 09:00 | |
| 21:00 |   3 3
| 15:00 | |
| 00:30 |  4 4
| 18:30 | |
| 06:00 |  5 5
| 00:00 |
Среди многочисленных проблем, которые встают перед «Золотым Пеликаном», довольно важной оказывается проблема местожительства бригад автобусов. При решении ее нужно минимизировать, учитывая требования расписания, общее время пребывания бригады вне дома. При этом исходят из совершенно очевидных финансовых соображений, так как оплата бригад не зависит от того, находятся ли они в пути или ожидают своего возвращения домой, в Мехико или в Акапулько. Кроме того, принимаются во внимание соображения социального порядка — не разлучать надолго главу семьи с остальными ее членами (правда, один из шоферов предлагал считать оптимумом как раз противоположное). С другой стороны, существуют физиологические пределы работы: ни одна бригада не должна пускаться в путь, не отдохнув в течение хотя бы четырех часов. Вместе с тем бригада не должна ждать рейса более чем 24 часа.
В этих условиях задача может быть сформулирована следующим образом. Где должны жить бригады и какие рейсы они должны обслуживать, чтобы суммарное время, которое все бригады теряют на ожидание обратного рейса, было бы минимальным при том ограничении, что время ожидания каждой бригады должно быть больше 4 часов и меньше 24 часов?
3.3.2. Алгоритм решения «Задачи о назначениях»
Предположим, например, что бригада живет в Мехико и обслуживает рейс c в направлении на Акапулько и рейс 2 в противоположном направлении. Эта бригада должна ждать в Акапулько 15,5 часа (от 17.30 до 09.00). Составим путем аналогичных расчетов две таблицы потерянного времени, считая в первом случае, что все бригады проживают в Мехико, а во втором,— что все они живут в Акапулько.
Таблица 6.1
Все бригады живут в Мехико
| a | 17,5 | 6,5 | |||
| b | 19,5 | 1,5 | 10,5 | ||
| c | 15,5 | 21,5 | 6,5 | ||
| d | 4,5 | 17,5 | |||
| e | 2,5 | 8,5 | 17,5 |
Таблица 6.2
Все бригады живут в Акапулько
| a | 18,5 | 5,5 | |||
| b | 16,5 | 10,5 | 1,5 | ||
| c | 20,5 | 14,5 | 5,5 | ||
| d | 7,5 | 18,5 | |||
| e | 9,5 | 3,5 | 18,5 |
Составим теперь на основе этих двух таблиц третью, каждый элемент которой будет являться меньшим из чисел, занимающих соответственные клетки в двух исходных таблицах. При этом мы не будем, однако, принимать во внимание числа, не превосходящие четырех (учитывая потребности бригады в отдыхе). Например, если нам представится выбор между числами а1 (место жительства в Мехико) и 1а (место жительства в Акапулько), то выбрать следует а1, дающее нам ожидание в 17,5 часа вместо 18,5 часа. Напротив, из b3 (Мехико) и 3b (Акапулько) мы выбираем 3b, хотя этому варианту и не соответствует меньшее время, ибо вариант b3 оставляет на отдых меньше 4 часов и потому неприемлем (или же свыше 24 часов, что мы предусмотрительно вовсе не учитываем в наших таблицах).
Таблица 6.3
Минимальные времена ожидания
| a | 17,5 | 5,5 | |||
| b | 16,5 | 10,5 | 10,5 | ||
| c | 15,5 | 14,5 | 5,5 | ||
| d | 4,5 | 17,5 | |||
| e | 9,5 | 8,5 | 17,5 |
Назовем назначением факт приписывания бригады одному из рейсов (скажем, al, 2a, а3 и т. д.). Очевидно, каждая бригада может быть назначена лишь на один прямой и на один обратный рейс. Таким образом, любое возможное решение задачи о назначениях может быть представлено таблицей, в клетках которой стоят числа 0 или 1, причем в каждой строке и в каждом столбце имеется ровно одна единица (символизирующая выбранное назначение).
Таблица 6.4
Пример возможного решения
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Например, решение, описываемое таблицей 6.4, соответствует рейсам 2а, b1, 5c, d3, e4, как это легко установить по предыдущим таблицам; при таком варианте трем бригадам следует жить в Мехико, а двум — в Акапулько. Суммарные потери времени будут составлять:
15 + 16 + 5,5 + 14 + 12 = 62,5 часа.
Для таблицы с пятью строками и пятью столбцами всего может быть
1×2×3×4×5 = 120
решений. Читатель может систематически их все перебрать — приятное развлечение в дождливое воскресенье, когда вы вынуждены ограничиться лишь мечтами об Акапулько. И среди этих 120 решений вы можете выбрать наилучшее.
При шести строках и шести столбцах мы имели бы для перечисления и сравнительной оценки уже
1×2×3×4×5×6 = 720
допустимых решений.
Если таблица имеет 20 строк и 20 столбцов, то число всех решений достигнет 2,4329×1023. Считая по минуте на составление каждого решения (с карандашом в руке это действительно можно проделывать достаточно быстро), мы получаем 4,63 миллиарда миллионов веков, необходимых для доведения дела до конца. Такие задачи, когда речь идет более чем о шести назначениях, не могут быть решены перечислением всех решений (за исключением отдельных, весьма частных случаев); чтобы благополучно закончить работу, следует применить некоторый метод расчета, некоторый алгоритм.
Причудливый и удручающий комбинаторный характер этих задач был преодолен путем использования венгерского метода (названного так в память знаменитой теоремы венгерского математика Кёнига).
Мы познакомим читателя с этим методом и покажем, как решить задачу о бригадах «Пеликана», хотя перечислением и сравнением всех 120 возможностей это можно было бы сделать за несколько часов, а действуя на основе интуиции, и еще быстрее.
Основная идея венгерского метода довольно проста, хотя некоторые строгие доказательства будут в этом предварительном изложении намеренно опущены. Мы сформулируем, однако, основной принцип, согласно которому оптимальность решения (или решений) задачи о назначениях не нарушается при уменьшении (или увеличении) всех выражающих время[1] элементов Cij строки таблицы (или ее столбца) на одну и ту же величину С. Это утверждение очевидно, так как решение может содержать в строке и в столбце только один единичный элемент (см. табл. 6.4). Таким образом, описанная операция уменьшает (или увеличивает) общую сумму (потерянное время или затраты, связанные с некоторым решением) на величину C, но не может изменить оптимальности решения.
Применим венгерский метод к нахождению оптимального назначения бригад «Пеликана». Любопытно, что для размещения единиц оптимального решения в таблице, аналогичной таблице 6.4, мы будем пытаться разместить нули в таблице 6.5, которая является точной копией таблицы 6.3.
Процесс решения расчленяется на шесть этапов.
Дата добавления: 2017-01-13; просмотров: 1246;
