Такое представление о геометрических фигурах, как частях плоскости, сохраняется и в определениях треугольника, многоугольника, круга и т.п.

Или можно представить модели нескольких углов и назвать это «углами»:

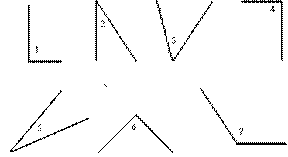
Требуется разбить эти углы на группы. И дети обязательно выделят группу прямых углов, остальные углы образуют класс непрямых углов (в традиционной системе).

Учащиеся должны находить прямые углы на различных моделях с помощью согнутого вчетверо листа бумаги произвольной формы – модели угла или с помощью чертежного угольника.

Прямоугольники

Среди всех четырехугольников выделим те, у которых все углы прямые. Среди них выделим те, у которых все стороны равны и получим КВАДРАТЫ. Дети не всегда ясно понимают, что любой квадрат является прямоугольником. На это нужно обратить внимание. Надо найти в окружающей обстановке те геометрические фигуры, которые вы изучаете.

Многоугольник В 3-м классе многоугольник обозначается буквами А В С D и т.д., делится на заданные фигуры, например на треугольники и четырехугольники. Учащиеся учатся находить общие стороны или отрезки, составлять из различных частей целый многоугольник.

Вопрос 22. Обучение учащихся общим приемам решения задач.

Все многообразие методических рекомендаций, связанных с обучением младших школьников решению задач, целесообразно рассматривать с точки зрения двух принципиально разных подходов.

Один нацелен на формирование у учащихся умения решать задачи определенных видов.

Цельдругого подхода – научить детей выполнять семантический и математический анализ текстовых задач, выявлять взаимосвязи между условием и вопросом, данными и искомыми, представлять эти связи в виде схематических и символических моделей. Средством организации этой деятельности могут быть специальные обучающие задания, включающие методические приемы сравнения. Выбора, преобразования, конструирования.

Для приобретения опыта в семантическом и математическом анализе задач (простых и составных) используется прием сравнения текстов. Для этой цели предлагаются задания:

v Чем похожи тексты задач? Чем отличаются? Какую задачу ты можешь решить? Какую не можешь? Почему?

1) На одном проводе сидели ласточки, а на другом – 7 воробьев. Сколько всего птиц сидело на проводах?

2) На одном проводе сидело 9 ласточек, а на другом 7 воробьев. Сколько всего птиц сидело на проводах?

v Подумай! Будут ли эти тексты задачами?

1) На одной тарелке 3 огурца, а на другой – 4. Сколько помидоров на двух тарелках?

2) На клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов на клумбе?

С целью формирования умения выбирать арифметические действия для решения задач, предлагаются в которых используются приемы:

Выбор схемы.

Выбор вопросов

v От проволоки длиной 15 см отрезали сначала 2 дм, потом еще 4дм.

a) Сколько всего дециметров проволоки отрезали?

b) На сколько дециметров меньше отрезали в первый раз, чем во второй?

c) На сколько дециметров проволока стала короче?

d) Сколько дециметров проволоки осталось?

3) Выбор выражений.

v На велогонках стартовало 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором – 6. Сколько спортсменов пришло к финишу?

Выбери выражение, которое является решением задачи:

6+4 6-4 70-6

70-6-4 70-4-6 70-4

4) Выбор условия к данному вопросу.

Подбери условия к данному вопросу и реши задачу.

Сколько всего детей занимается в студии?

а) В студии 30 детей, из них 16 мальчиков.

б) В студии мальчики и девочки. Мальчиков на 7 меньше, чем девочек.

в) В студии 8 мальчиков и 20 девочек.

г) В студии 8 мальчиков, а девочек на 2больше.

д) В студии занимаются 8 мальчиков, а девочек на 2 меньше.

Выбор данных.

v На аэродроме было 75 самолетов. Сколько самолетов осталось?

Выбери данные, которыми можно дополнить условие задачи, чтобы ответить на поставленный вопрос:

а) Утром прилетело 10 самолетов, а вечером улетело 30.

б) Улетело на 20 самолетов больше, чем было.

в) Улетело сначала 30 самолетов, а потом 20.