Площадь многоугольника

Формулы для вычисления площади прямоугольника, треугольника, параллелограмма были выведены давно. В геометрии их обосновывают, исходя из определения площади, при этом численное значение площади называют площадью, а численное значение длины отрезка - длиной.

Теорема. Площадь прямоугольника равна произведению длин соседних его сторон.

Напомним, что слово «площадь» в этой формулировке означает численное значение площади, а слово «длина» - численное значение длины отрезка.

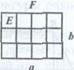
Доказательство. Если F- данный прямоугольник,а числа а, b-длины его сторон, то S(F) = а·b. Докажем это.

Пусть а и b - натуральные числа. Тогда прямоугольник Fможно разбить на единичные квадраты (рис. 3): F = Е ⊕ Е ⊕ Е ⊕ ... ⊕ Е. Всего их а·b, так как имеем b рядов, в каждом из которых а квадратов. Отсюда

S(F) = S(Е) + S(Е)+…+ S(Е)= а·b·S(Е)= а·b.

а·b слаг. 1

Пусть теперь а и b - положительные рациональные числа: а=m/n, b=p/q, где т, п, р, q - натуральные числа.

Приведем данные дроби к общему знаменателю: а= mq/nq, b=np/pq

Разобьем сторону единичного квадрата Е на пq равных частей. Если через точки деления провести прямые, параллельные сторонам, то квадрат Е разделится на (пq)^г более мелких квадратов. Обозначим площадь каждого такого квадрата Е1. Тогда S(Е) = (пq)^г S(Е1), а поскольку S(Е) = 1, то

S(Е1)= 1/(пq)^г.

Так как а= mq/nq, b=np/pq, то отрезок длиной 1/nq укладывается настороне а точно mq раз, а на стороне b – точно np раз. Поэтому данный прямоугольник F будет состоять из mq·np квадратов Е1. Следовательно,

S(F) = mq·np· S(Е1) = mq·np(1/(пq)^г= ( mq·np)/( np·np)=m/p· p/q= а·b.

Таким образом доказано, что если длины сторон прямоугольника выражены положительными рациональными числами а и b, то площадь этого прямоугольника вычисляется по формуле S(F) = а·b.

Случай, когда длины сторон прямоугольника выражаются положительными действительными числами, мы опускаем.

Из этой теоремы вытекает следствие: площадь прямоугольного треугольника равна половине произведения его катетов.

Теорема. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Доказательство. Пусть АВСD - параллелограмм, не являющийся прямоугольником (рис. 4). Опустим перпендикуляр СЕ из вершины С на прямую АD. Тогда S(АВСЕ) = S(АВСD) + S(СDЕ).

Опустим перпендикуляр ВF из вершины В на прямую АD. Тогда S (АВСЕ) = S (ВСЕF) + S (АВF).

Так как треугольники АВF и СDЕ равны, то равны и их площади.

Отсюда следует, что S(АВСD) = S(ВСЕF), т.е. площадь параллелограмма АВСD равна площади прямоугольника ВСЕF и равна ВС·ВР, а так как ВС = АD, то S(АВС) = АD ·ВF.

Из этой теоремы вытекает следствие: площадь треугольника равна половине произведения его стороны на проведенную к ней высоту.

Теорема. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Если периметр правильного многоугольника обозначить буквой Р, радиус вписанной окружности – r, а площадь правильного многоугольника – S, то, согласно данной теореме, S = 1/2· P· s.

Доказательство. Пусть АВСВ - параллелограмм, не являющийся прямоугольником (см. рис.). Опустим перпендикуляр СЕ из вершины С на прямую АD. Тогда S(АВСЕ) = S(АВСD) + S(СDЕ).

Опустим перпендикуляр ВF из вершины В на прямую АВ.

Тогда S(АВСЕ)= S(ВСЕF) + S(АВF).

Так как треугольники АВF и СDЕ равны, то равны и их площади.

Отсюда следует, что S(АВСD) = S(ВСЕF), т.е. площадь параллелограмма АВСD равна площади прямоугольника ВСЕF и равна ВС·ВF, а так как ВС = АD, то S(АВСD) = АD·ВF.

В С

Из этой теоремы вытекает следствие: площадь треугольника равна половине произведения его стороны на проведенную к ней высоту.

А F D E

Заметим, что слова «сторона» и «высота» обозначают численные значения длин соответствующих отрезков.

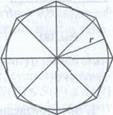
Теорема: Площадь правильного многоугольника равна половине произведения его периметра на радиус вписанной окружности.

Если периметр правильного многоугольника обозначить буквой Р, радиус вписанной окружности – r, а площадь – S, то, согласно данной теореме, S = 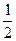• Р• r.

Доказательство. Разобьем правильный n-угольник на n треугольников, соединяя отрезками вершины n-угольника с центром вписанной окружности. Эти треугольники равны. Площадь каждого из них равна 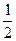• а• r,

где a - сторона правильного многоугольника.

Тогда площадь многоугольника равна 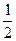• а• r•n, но а•n = Р. Следовательно, S = 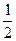• Р• r.

Если F- произвольный многоугольник, то его площадь находят, разбивая многоугольник на треугольники (или другие фигуры, для которых известны правила вычисления площади). В связи с этим возникает вопрос: если один и тот же многоугольникпо-разному разбить на части и найти их площади, то будут ли полученные суммы площадей частей многоугольника одинаковыми? Доказано, что условиями, сформулированными в определении площади, площадь всякого многоугольника определена однозначно.

Кроме равенства и равновеликости фигур в геометрии рассматривают отношение равносоставленности. С ним связаны важные свойства фигур.

Многоугольники F₁ и F₂ называются равносоставленными, еслиих можно разбить на соответственно равные части.

Например, равносоставлены параллелограмм АВСD и прямоугольник FВСЕ, так как параллелограмм состоит из фигур F₁ и F₂,а прямоугольник - из фигур F₂ и F₃, причем F₁ = F₂.

Нетрудно убедиться в том, что равносоставленные фигуры равновелики.

Венгерским математиком Ф.Бойяи и немецким любителем математики П.Гервином была доказана теорема: любые два равновеликих многоугольника равносоставлены. Другими словами, если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.

Теорема Бойяи-Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.

Доказательство сложное. Мы докажем только утверждение о том, что всякий треугольник равносоставлен с некоторым прямоугольником, т.е. всякий треугольник можно перекроить в равновеликий ему прямоугольник.

В

Р К Т L M

А D C

Пусть дан треугольник АВС. Проведем в нем высоту DВ и среднюю линию КL. Построим прямоугольник, одной стороной которого является АС, а другая лежит на прямой КL. Так как пары треугольников АРК и КВТ, а также СLМ и ТВL равны, то треугольник АВС и прямоугольник АРМС равносоставлены.

<87 88 899091 92 93 >

Дата добавления: 2016-05-11; просмотров: 2380;