Лекция 30. Неравенства с двумя переменными

План:

1. Неравенства с двумя переменными. Способы решения системы двух неравенств с двумя переменными: аналитический способ и графический способ.

2. Системы двух неравенств с двумя переменными: запись результата решения.

3. Совокупности неравенств с двумя переменными.

НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕН­НЫМИ. Предикат вида f₁(х, у)>< f₂(х, у), хÎХ, уÎ У, где f₁(х, у) и f₂(х, у) - выраже­ния с переменными х и у, определенные на множестве ХхУ называется неравенст­вом с двумя переменными (с двумя неизвестными)х и у. Ясно, что любое нера­венство вида с двумя переменными можно записать в виде f(х, у) > 0, хÎХ, уÎ У. Решением неравенствас двумя переменными называется пара значений пере­менных, обращающая неравенство в верное числовое неравенство. Известно, что пара действительных чисел (х, у) однозначно определяет точку координатной плос­кости. Это дает возможность изобразить решения неравенства или системы нера­венств с двумя переменными геометрически, в виде некоторого множества точек коорди­натной плоскости. Если уравнение.

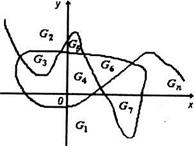
f(х, у) = 0 определяет некоторую линию на координат­ной плоскости, то множество точек плоско­сти, не лежащих на этой линии, состоит из конечного числа областей С₁, С₂,..., С_п (рис. 17.8). В каждой из областей С, функция f(х, у) отлична от нуля, т.к. точки, в которых f(х, у) = 0 принадлежат границам этих областей.

Теорема 17.6. В каждой из областей G(/ = 1,2,...), на которые линия f(х, у) = 0 делит координатную плоскость, функция f(х, у) либо положи­тельна, либо отрицательна.

Доказательство этой теоремы опускается.

Пример 17.14. Изобразите на координатной плоскости множество решений нера­венства

у{у + 2) < х + 3.

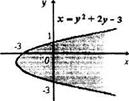
Решение. Преобразуем неравенство к виду х > у² + 2у - 3. Построим на координат­ной плоскости параболу х = у² + 2у - 3. Она разобьет плоскость на две области G₁ и G₂ (рис. 17.9). Так как абсцисса любой точки, лежащей правее параболы х = у² + 2у - 3, больше, чем абсцисса точки, имеющей ту же ординату, но лежащей на параболе, и т.к. неравенство х>у^г + 2у -3 нестрогое, то геометрическим изображением решений данно­го неравенства будет множество точек плоскости, лежащих на параболе х = у² + 2у - 3 и правее нее (рис. 17.9).

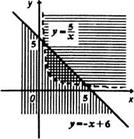
Рис. 17.10

Пример 17.15.Изобразите на координатной плоскости множество решений систе­мы неравенств

х > 0,

у > 0,

ху > 5,

х + у <6.

Решение. Геометрическим изображением решения системы неравенств х > 0, у > 0 является множество точек первого координатного угла. Геометрическим изображением решений неравенства х + у < 6 или у < 6 - х является множество точек, лежащих ниже прямой и на самой прямой, служащей графиком функции у = 6 - х. Геометрическим изображением решений неравенства ху > 5 или, поскольку х > 0 неравенства у > 5/х является множество точек, лежащих выше ветви гиперболы, служащей графиком функ­ции у = 5/х. В итоге получаем множество точек координатной плоскости, лежащих в первом координатном углу ниже прямой, служащей графиком функции у = 6 - х, и выше ветви гиперболы, служащей графиком функции у = 5х (рис. 17.10).