Решение неравенств с одной переменной
Решим неравенство 5х - 5 < 2х - 16, х € R, и обоснуем все преобразования, которые мы будем выполнять в процессе решения.
| Преобразования | Обоснование преобразования |
| 1. Приведем выражении 2x в левую часть, а число -5 в правую, поменяв их знаки на противоположные: 5x-2x < 16+5 | Воспользовались следствием 2 из теоремы 3, получили неравенство, равносильное данному |
| 2. Приведем подобные члены в левой и правой частях неравенства: 3х< 21 | Выполнили тождественные преобразования выражений в левой и правой частях неравенства - они не нарушили равносильности неравенств: данного и исходного. |
| 3. Разделим обе части неравенства на 3: х<7. | Воспользовались следствием из теоремы 4, получили неравенство, равносильное исходному |
Решением неравенства х < 7 является промежуток (-∞, 7) и, следовательно, множеством решений неравенства 5х - 5 < 2х + 16 является промежуток (-∞, 7).
Упражнения
1. Установите, какие из следующих записей являются неравенствами с одной переменной:
а) -12 - 7х < 3x + 8; г) 12х + 3(х- 2);
б) 15(x + 2)>4; д) 17-12·8;
в) 17-(13 + 8) < 14-9; е) 2х2 + 3x-4> 0.
2.Является ли число 3 решением неравенства 6(2х + 7) < 15(х + 2), х € R? А число 4,25?
3.Равносильны ли на множестве действительных чисел следующие пары неравенств:
а) -17х< -51 и х > 3;
б) (3x-1)/4 >0 и 3х-1>0;
в) 6-5x >-4 и х<2?
4. Какие из следующих высказываний истинны:
а) -7 х < -28 => x>4;
б) x < 6 => x < 5;
в) х < 6 => х < 20?
5.Решите неравенство 3(x - 2) - 4(х + 1) < 2(х - 3) - 2 и обоснуйте все преобразования, которые будете при этом выполнять.
6.Докажите, что решением неравенства 2(х + 1) + 5 > 3 - (1 - 2х) является любое действительное число.
7.Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3(2 - х) - 2 > 5 - 3х.
8.Одна сторона треугольника равна 5 см, а другая 8 см. Какой может быть длина третьей стороны, если периметр треугольника:
а) меньше 22 см;
б) больше 17 см?
 ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ.Для графического решения неравенства f (х) > g (х) нужно построить графики функций
ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ.Для графического решения неравенства f (х) > g (х) нужно построить графики функций
у = f (х) = g (х) и выбрать те промежутки оси абсцисс, на которых график функции у = f (х) расположен выше графика функции у = g (х).
Пример 17.8.Решите графически неравенство х2 - 4 > 3х.
| У - х* - 4 |
Решение. Построим в одной системе координат графики функций
у = х2- 4 и у = Зх (рис. 17.5). Из рисунка видно, что графики функций у = х2 - 4 расположен выше графика функции у = 3х при х < -1 и х > 4, т.е. множество решений исходного неравенства есть множество
(- ¥; -1) È (4; +оо).
Ответ: х Î (- оо; -1) и (4;+ оо ).
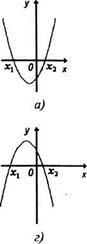
Графиком квадратичной функции у = ах2 + bх + с является парабола с ветвями, направленными вверх, если а > 0, и вниз, если а < 0. При этом возможны три случая: парабола пересекает ось Ох (т.е. уравнение ах2 + bх + с = 0 имеет два различных корня); парабола касается оси х (т.е. уравнение ах2 + bх + с = 0 имеет один корень); парабола не пересекает ось Ох (т.е. уравнение ах2 + bх + с = 0 не имеет корней). Таким образом, возможны шесть положений параболы, служащей графиком функции у = ах2 + bх + с (рис. 17.6). Используя эти иллюстрации, можно решать квадратные неравенства.
|
Пример 17.9. Решите неравенство: а) 2хг + 5х - 3 > 0; б) -Зх2 - 2х - 6 < 0.
Решение, а) Уравнение 2х2 + 5х -3 = 0 имеет два корня: х, = -3, х2 = 0,5. Парабола, служащая графиком функции у = 2х2 + 5х -3, показана на рис. а. Неравенство 2х2 + 5х -3 > 0 выполняется при тех значениях х, при которых точки параболы лежат выше оси Ох: это будет при х < хх или при х > хг> т.е. при х < -3 или при х > 0,5. Значит, множество решений исходного неравенства есть множество (- ¥; -3) и (0,5; + ¥).
б) Уравнение -Зх2 + 2х- 6 = 0 не имеет действительных корней. Парабола, служащая графиком функции у = - 3х2 - 2х - 6, показана на рис. 17.6 Неравенство -3х2 - 2х - 6 < О выполняется при тех значениях х, при которых точки параболы лежат ниже оси Ох. Поскольку вся парабола лежит ниже оси Ох, то множество решений исходного неравенства есть множество R.
НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ.При решении данных неравенств следует иметь в виду, что:
| f(х) | =
f(х) , если f(х) ³ 0,
- f(х) , если f(х) < 0,
При этом область допустимых значений неравенства следует разбить на интервалы, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. Затем, раскрывая модули (с учетом знаков выражений), нужно решать неравенство на каждом интервале и полученные решения объединять в множество решений исходного неравенства.
Пример 17.10. Решите неравенство:
|х -1| + |2- х| > 3+х.
Решение. Точки х = 1 и х = 2 делят числовую ось (ОДЗ неравенства (17.9) на три интервала: х < 1, 1 £ х £.2, х > 2. Решим данное неравенство на каждом из них. Если х < 1, то х - 1 < 0 и 2 – х > 0; поэтому |х -1| = - (х - I), |2 - х | = 2 - х. Значит, неравенство (17.9) принимает вид: 1- х + 2 - х > 3 + х, т.е. х < 0. Таким образом, в этом случае решениями неравенства (17.9) являются все отрицательные числа.
Если 1 £ х £.2, то х - 1 ³ 0 и 2 – х ³ 0; поэтому | х- 1| = х - 1, |2 - х| = 2 – х. .Значит, имеет место система:
1 £ х £.2
х – 1 + 2 – х > 3 + х,
или
1 £ х £.2
х < - 2
Полученная система неравенств решений не имеет. Следовательно, на интервале [ 1; 2] множество решений неравенства (17.9) пусто.
Если х > 2, то х - 1 >0 и 2 – х <0; поэтому | х - 1| = х- 1, |2-х| = -(2- х). Значит, имеет место система:
х > 2,
х -1 + х – 2 > 3+х,
или
х > 2,
х > 6 или
х > 6
Объединяя найденные решения на всех частях ОДЗ неравенства (17.9), получаем его решение - множество (-¥; 0) È (6; +оо).
Иногда полезно воспользоваться геометрической интерпретацией модуля действительного числа, согласно которой | а | означает расстояние точки а координатной прямой от начала отсчета О, а | а - b | означает расстояние между точками а и b на координатной прямой. Кроме того, можно использовать метод возведения в квадрат обеих частей неравенства.
Теорема 17.5. Если выражения f (х) и g (х) при любых х принимают только неотрицательные значения, то неравенства f (х) > g (х) и f (х) ² > g (х) ² равносильны.
58. Основные выводы § 12
В данном параграфе мы определили следующие понятия:
- числовое выражение;
- значение числового выражения;
- выражение, не имеющее смысла;
- выражение с переменной (переменными);
- область определения выражения;
- тождественно равные выражения;
- тождество;
- тождественное преобразование выражения;
- числовое равенство;
- числовое неравенство;
- уравнение с одной переменной;
- корень уравнения;
- что значит решить уравнение;
- равносильные уравнения;
- неравенство с одной переменной;
- решение неравенства;
- что значит решить неравенство;
- равносильные неравенства.
Кроме того, мы рассмотрели теоремы о равносильности уравнений и неравенств, являющиеся основой их решения.
Знание определений всех названных выше понятий и теорем о равносильности уравнений и неравенств - необходимое условие методически грамотного изучения с младшими школьниками алгебраического материала.
Дата добавления: 2016-05-11; просмотров: 3449;
