Лекция 12. Текстовая задача и процесс ее решения
План:
1. Решение задач «на части»
2. Решение задач на движение
3. Основные выводы
32. Решение задач «на части»
Само название вида задач говорит о том, что рассматриваемые в них величины состоят из частей. В некоторых из них части представлены явно, в других эти части надо суметь выделить, приняв подходящую величину за 1 часть и определив, из скольких таких частей состоят другие величины, о которых идет речь в задаче.
При решении таких задач арифметическим методом чаше всего используют вспомогательные модели, выполненные с помощью отрезков или прямоугольников.
Задача 1. Для варки варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара надо взять па 10 кг ягод?
Решение. В задаче речь идет о массе ягод и массе сахара, необходимых для варки варенья. Известно, что всего ягод 10 кг и что на 2 части ягод надо брать 3 части сахара. Требуется найти массу сахара. чтобы сварить варенье из 10 кг ягод.
Изобразим при помощи отрезка данную массу ягод (рис. 45). Тогда половина этого отрезка представляет собой массу ягод, которая приходится на 1 часть.
В 10 кг

С ?
Рис. 45
Сахара, по условию задачи, надо 3 таких части. Запишем решение по действиям с пояснением:
1) 10:2 = 5 (кг) - столько килограммов ягод приходится на каждую часть;
2) 5 ×3 = 15 (кг) - столько надо взять сахара.
Вспомогательную модель к данной задаче можно было выполнить при помощи прямоугольников (рис. 46).
10 кг ?


Рис. 46
Задача 2. В первой пачке было на 10 тетрадей больше, чем во второй. Всего было 70 тетрадей. Сколько тетрадей было в каждой пачке?
Решение. В задаче рассматриваются две пачки тетрадей. Всего тетрадей 70. В одной пачке тетрадей на 10 больше, чем во второй. Требуется узнать, сколько тетрадей было в каждой пачке.
Изобразим при помощи отрезка количество тетрадей во второй пачке. Тогда тетради в первой пачке можно представить в виде отрезка, который больше второго (рис. 47). По чертежу видно, что если тетради
10 т.

Рис. 47
во второй пачке составляют 1 часть всех тетрадей, то тетради в первой составляют также 1 часть и еще 10 тетрадей.
Если эти 10 тетрадей убрать из первой пачки, то в пачках тетрадей станет поровну - столько, сколько во второй пачке.
Запишем решение задачи по действиям с пояснением.
1) 70-10 = 60 (тетр.) - столько тетрадей приходится на 2 равные части, или столько было бы тетрадей в двух пачках, если бы их было поровну - столько, сколько во второй пачке.
2) 60:2 = 30 (тетр.) - столько тетрадей приходится на 1 часть, или столько тетрадей было во второй пачке.
3) 30 +10 — 40 (тетр.) - столько тетрадей было в первой пачке.
Вспомогательная модель подсказывает и второй способ решения данной задачи. Если за I часть принять тетради в первой пачке, то чтобы во второй стало столько же, надо к ней добавить 10 тетрадей. И тогда решение будет таким:
1) 70+10 = 80 (тетр.)
2) 80:2 = 40 (тетр.)
3) 40-10 = 30 (тетр.)
Существует и третий арифметический способ решения данной задачи. Разделим 10 тетрадей пополам и одну половину оставим к первой пачке, а другую добавим во вторую. Тогда тетрадей в пачках станет поровну и можно, разделив 70 на 2 равные части, узнать, сколько тетрадей в каждой такой пачке, а затем их первоначальное количество в каждой пачке.
1) 10:2 = 5 (тетр.) - столько тетрадей надо переложить из первой
пачки во вторую, чтобы в них тетрадей стало поровну.
2) 70:2 = 35 (тетр.) - столько тетрадей в каждой пачке, если из первой переложить во вторую 5 тетрадей.
3) 35 + 5 = 40 (гетр.) - столько тетрадей в первой пачке.
4) 35-5 = 30 (тетр.) - столько тетрадей во второй пачке.
Задача 3. Сумма двух чисел 96, а разность 18. Найдите эти числа.
Решение. В этой задаче требуется найти два числа по их сумме и разности. Так как разность искомых чисел равна 18, то одно число больше другого на 18. Получаем задачу, аналогичную задаче 2: «Одно число больше другого па 18. Сумма чисел равна 96. Найти эти числам Решить ее можно тремя арифметическими способами.
Задача 4. В двух кусках ткани одинаковое количество материи. После того как от одного куска отрезали 18 м, а от другого 25 м, в первом куске осталось вдвое больше ткани, чем во втором. Сколько метров ткани было в каждом куске первоначально?
Решение. Объекты задачи - два куска ткани одинаковой длины От первого отрезали 18 м, от второго 25 м. После этого в первом осталось вдвое больше ткани, чем во втором. Требование задачи - найти первоначальное количество метров ткани в каждом куске.
Изобразим куски ткани при помощи отрезков одинаковой длины, а затем покажем на них то количество ткани, которое отрезали
| 18 м |
| I |
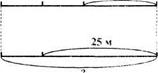
|
| II |
| Рис. 48 |
и которое осталось. Если количество ткани, которое осталось во втором куске, - это 1 часть, то количество оставшейся ткани в первом куске - это 2 таких части По чертежу (рис. 48) видно, что на 1 часть приходится количество ткани, которое легко найти. Запишем найденное решение по действиям:
1) 25-18 = 7 (м) - на столько больше ткани отрезали от второго
куска, или количество ткани, которое осталось во втором куске
2) 7 + 25 -- 32 (м) - столько ткани было первоначально во втором
куске (и, следовательно, в первом) куске.
Упражнения
1. Изобразите при помощи отрезков ситуации:
а) купили р кг яблок, а груш на 1 кг больше;
б) купили р кг яблок, а груш в 2 раза больше.
Какими могут быть требования к данным ситуациям? Для каждого случая постройте модель и обозначьте на ней требования.
2. Требуется смешать 3 части песка и 2 части цемента. Сколько
цемента и песка в отдельности надо взять, чтобы получить 30 кг
смеси?
3, Установите соответствие между вспомогательными моделями и следующими задачами; используя модели, решите задачи:
а) В двух пакетах было 15 яблок. Когда из одного пакета взяли 3 яблока, в нем
осталось в 2 раза меньше яблок, чем в другом. Сколько яблок было в каждом пакете?
б) В трех пакетах лежит 20 яблок, причем в одном пакете их в 2 раза меньше, чем в каждом из двух других. Сколько яблок в каждом пакете?
в) У двух мальчиков было 8 яблок. Когда один съел одно яблоко, а другой 3 яблока, у них осталось яблок поровну. Сколько яблок было у каждого?
4. Решите следующие задачи, построив на этапе анализа вспомогательные модели; решение запишите по действиям с пояснением:
а) Мама дала трем девочкам 12 конфет и предложила разделить их так, чтобы младшая получила в 3 раза, а средняя в 2 раза больше старшей. Сколько конфет достанется каждой?
б) На двух тарелках лежало 9 яблок. Когда с одной тарелки взяли одно яблоко, то на этой тарелке осталось яблок в 3 раза больше, чем на другой. Сколько яблок было на каждой тарелке?
в) У моего брата было в 6 раз больше орехов, чем у меня. После того как он отдал 10 орехов сестре, у нас орехов стало поровну. Сколько орехов было у меня и у брата первоначально?
г) Полсотни яблок разложили в корзину и два пакета. В корзину положили на 14 яблок больше, чем в каждый пакет. Сколько яблок в корзине и в пакете?
д) Школьник прочитал 18 страниц за три дня. Если бы он в первый день прочитал на одну страницу больше, а во второй день на 4 страницы меньше, то каждый день он читал бы поровну. По сколько страниц читал школьник каждый день?
5. Постройте вспомогательные модели и с их помощью найдите решения следующих задач:
а) На одной полке на 6 книг больше, чем на другой. Сколько книг нужно переложить с одной полки на другую, чтобы книг стало поровну?
6} Если с одной полки переложить на другую 6 книг, то на обеих полках книг будет поровну. На сколько книг на одной полке больше, чем на другой?
в) На одной полке на 6 книг больше, чем на другой. На сколько книг будет больше на одной полке, чем на другой, если с первой полки переложили на другую 10 книг?
г) На первой полке на 6 книг больше, чем на второй. На сколько книг будет на первой полке больше, если со второй полки переложить на первую 10 книг?
6. Поиск плана решения проведите по вспомогательной модели; решение запишите по действиям; выполните проверку найденного решения:
а) В двух бидонах 28 л краски. Если из одного взять 3 л, а в другой добавить 2 л, то в первом станет на 7 л краски больше, чем во втором. Сколько краски в каждом бидоне?
б) На складе в три раза больше муки, чем в магазине. Если со склада взять 850 т муки, а магазином будет продано 50 т муки, то и на складе, и в магазине муки останется поровну. Сколько муки на складе и сколько в магазине?
в) У Наташи на 15 открыток больше, чем у Сережи. Детям подарили еще по 6 открыток У Наташи стало в 2 раза больше открыток, чем у Сережи. Сколько открыток было у каждого первоначально?
7. Решите различными арифметическими способами:
а) В двух книжных шкафах было 1536 книг. Когда из одного взяли 156 книг, а из другого в три раза больше, то книг в шкафу стало поровну. Сколько книг было в каждом шкафу первоначально?
б) Площадь земли, засеянная пшеницей, в 6 раз больше площади, засеянной ячменем, а площадь, засеянная рожью, в 3 раза меньше площади, засеянной пшеницей. Сколько гектаров земли засеяно каждой культурой, если пшеницей засеяно на 480 га больше, чем рожью?
Дата добавления: 2016-05-11; просмотров: 6614;
