Рівномірне наближення функцій

Нехай 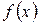– задана на відрізку 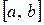неперервна функція. Кажуть, що поліном 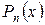наближає функцію 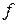на відрізку 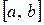з точністю ε, якщо 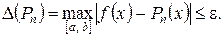Таким чином, величина 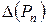грає роль похибки наближення.

Розглянемо наступну задачу: серед усіх поліномів фіксованого степеня n знайти поліном 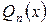, для якого величина похибки рівномірного наближення мінімальна, тобто 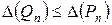для будь-якого 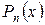степеня n. Поставлена задача називається задачею про найкраще рівномірне наближення, в якому шуканий поліном 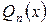є поліномом найкращого рівномірного наближення.

Доведено, що для будь-якої неперервної на відрізку 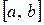функції 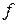поліном найкращого рівномірного наближення 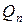степеня n існує і він є єдиним.

У більшості реальних випадків задача про найкраще рівномірне наближення неперервної функції 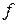є дуже складною. Для її розв’язання розроблені спеціальні числові методи, які реалізовані у виді стандартних програм. У багатьох ситуаціях достатньо обмежитися находженням полінома, близького до найкращого або просто знайти поліном, що рівномірно наближає функцію 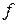з заданою точністю ε.