Асимптотика циліндричних функцій.

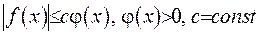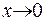Встановимо поведінку циліндричних функцій у нулі та на нескінченності. Попередньо введемо символ Ландау, який будемо вживати наступним чином. Якщо при , то будемо писати 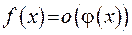. Якщо ця оцінка має місце при 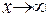, то будемо записувати 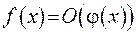. (Мається на увазі, що функція 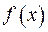поводить себе так, як функція ).

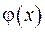Розглянемо зображення функції Беселя за допомогою ряду (6.68) та розпишемо ряд, що входить до співвідношення:

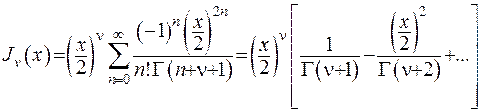
Як бачимо, в околі нуля - 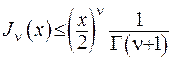. Якщо ввести позначення 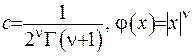, то за допомогою символу Ландау знайдемо:

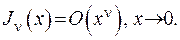(6.85)

Можна показати, що при будь-якому значенні порядку 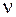функції Неймана та Ханкеля мають поведінку:

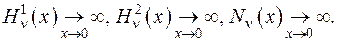
Встановимо їх поведінку, коли 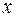прямує до нескінченності. З цією метою скористаємося встановленими раніше фактами:

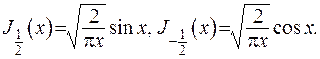
З цього випливає, що при 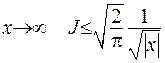та .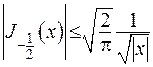

Якщо взяти 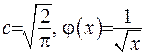(якщо 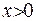, то модуль можна усунути), то матимемо: 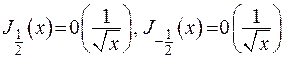. Можна стверджувати, що для будь-якого порядку 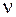поведінка функції Беселя при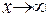

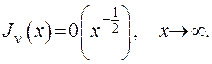(6.86)

Так сама поведінка на нескінченності має місце для додатніх 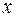у інших функцій - .

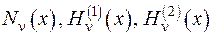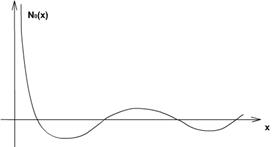
Розглянемо найбільш важливі випадки функції Беселя у графічному зображенні: