Приклади задач математичної фізики, що приводять до використання спеціальних функцій.
Функції Беселя.
Розв’язати задачу стаціонарної теплопровідності усередині обмеженого циліндру 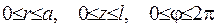 , якщо
, якщо
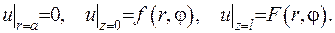
Розв’язання задачі.
Розшукуємо розв’язок поставленої задачі у вигляді
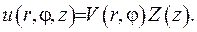
Підставимо це зображення до рівняння
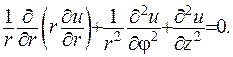
Розподіляючи змінні, обираємо для 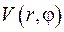 рівняння
рівняння
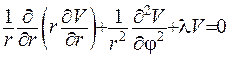
З граничною умовою

Для функції 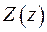 отримаємо рівняння
отримаємо рівняння

Далі будемо вважати, що має місце подання
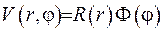
З цього випливає
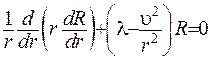
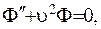
де 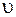 - стала розподілення.
- стала розподілення.
Для функції 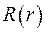 маємо рівняння Беселя
маємо рівняння Беселя
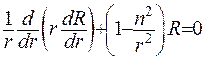
з граничною умовою
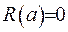
Та природною умовою обмеженості у нулі
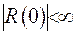
Звідці випливає 
Гранична умова при 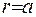 дає
дає
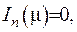 де
де 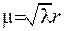
Нехай  корні цього рівняння.
корні цього рівняння.
Таким чином, крайова задача для 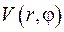 має власні значення
має власні значення 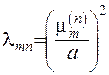 , якім відповідають власні функції
, якім відповідають власні функції
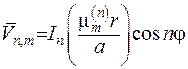
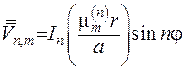
що утворюють дві ортогональні системи функції, для яких
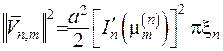
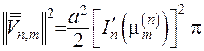 ,
,
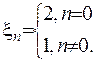
Загальний розв’язок задачі має вигляд

де 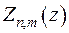 розв’язок рівняння
розв’язок рівняння 
Шукану функцію 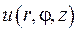 можна зобразити у вигляді суми двох функцій
можна зобразити у вигляді суми двох функцій
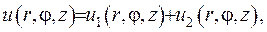 де
де 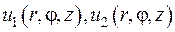 - гармонічні функції, що задовольняють умовам
- гармонічні функції, що задовольняють умовам
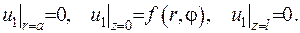
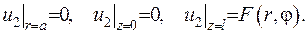
Покажемо як побудувати функцію 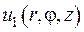 . Для цього випадку
. Для цього випадку

Задовольнимо крайову умову при 
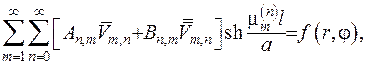
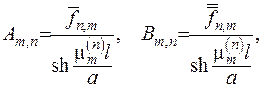
 (*)
(*)
Отже, наприкінці запишемо розв’язок вихідної задачі у вигляді
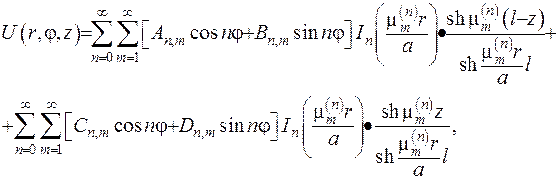
де 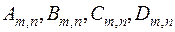 - коефіцієнти розкладу функції
- коефіцієнти розкладу функції 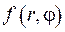 та
та 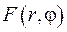 вигляду (*).
вигляду (*).
Поліноми Лежандра.
Розв’язати задачу про коливання струни довжиною 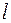 , яка закріплена одним кінцем на нерухомій опорі та може вільно обертатися навколо точки опори.
, яка закріплена одним кінцем на нерухомій опорі та може вільно обертатися навколо точки опори.
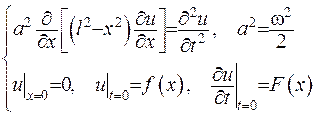
 - кутова швидкість.
- кутова швидкість.
Розшукуватиме розв’язок у вигляді
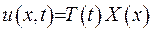
Відповідно до схеми методу розподілення змінних
Підставляючи в (25), маємо:
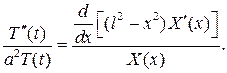
Позначаючи обидві частини цієї рівності через 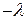 , одержимо два рівняння
, одержимо два рівняння
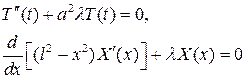 (29)
(29)
Вважаючи 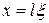 , перетворимо рівняння (30) до вигляду
, перетворимо рівняння (30) до вигляду
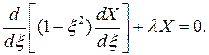 (31)
(31)
Це є рівняння Лежандра.
По своєму фізичному значенню зсув струни 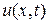 повинно залишатися обмеженим в проміжку
повинно залишатися обмеженим в проміжку 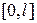 . Тому потрібно знайти такі рішення рівняння (30), які обмежені в цьому проміжку, включаючи його кінці. На початку цього розділу було показано, що при
. Тому потрібно знайти такі рішення рівняння (30), які обмежені в цьому проміжку, включаючи його кінці. На початку цього розділу було показано, що при 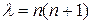 , де
, де 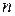 - ціле позитивне число, рівняння Лежандра (31) в проміжку [-1, 1] має рішення, обмежене в точках
- ціле позитивне число, рівняння Лежандра (31) в проміжку [-1, 1] має рішення, обмежене в точках  . Це рішення є поліном Лежандра
. Це рішення є поліном Лежандра 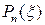 . Отже, повертаючись до змінної
. Отже, повертаючись до змінної 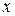 , ми можемо стверджувати, що
, ми можемо стверджувати, що
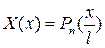 (32)
(32)
є рішення рівняння (30), обмежене в точках 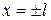 при
при 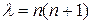 .
.
Задовольняючи граничній умові (26), одержимо
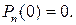
Це можливо, коли 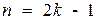 , де
, де 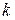 - ціле додатне число.
- ціле додатне число.
Таким чином, нетривіальні рішення рівняння (30) при граничних умовах
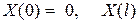 – ограничено (33)
– ограничено (33)
можливі лише при значеннях
 (34)
(34)
Цим власним числам відповідають власні функції
 (35)
(35)
які утворюють ортогональну систему функцій на відрізку 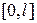 .
.
При  загальне рішення рівняння (29) має вигляд
загальне рішення рівняння (29) має вигляд
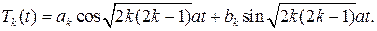 (36)
(36)
В силу (28), одержимо, що функції 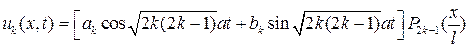 (37)
(37)
задовольняють рівнянню (25) і граничній умові (26) при будь-яких 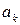 і
і 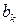 . Для рішення задачі складаємо ряд
. Для рішення задачі складаємо ряд
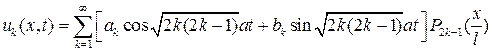 (38)
(38)
і вимагаємо, щоб виконувалися початкові умови (27):
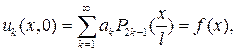 (39)
(39)
 (40)
(40)
Припускаючи, що ряд (39) сходиться рівномірно, ми можемо визначити коефіцієнти 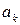 , помноживши обидві частини рівності (39) на
, помноживши обидві частини рівності (39) на 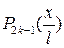 і проінтегрувати по х в інтервалі від 0 до
і проінтегрувати по х в інтервалі від 0 до 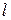 ; тоді беручи до уваги ортогональність власних функцій, одержимо
; тоді беручи до уваги ортогональність власних функцій, одержимо
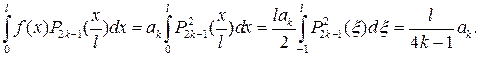
Звідси
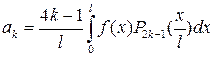 (41)
(41)
Аналогічно знайдемо
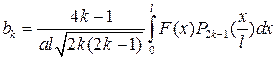 (42)
(42)
Таким чином, рішення задачі дається поряд (38), де 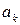 і
і 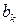 визначаються формулами (41) і (42).
визначаються формулами (41) і (42).
Переписавши рішення (38) у вигляді
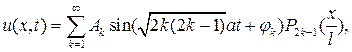 (43)
(43)
ми бачимо, що малі коливання струни, що обертається, складаються з гармонійних коливань. Частота коливань 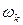
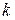 -го обертону виражається формулою
-го обертону виражається формулою

Звідси витікає, що частоти коливань залежать від кутової швидкості 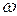 і не залежать від довжини струни і її густини (до тих пір, поки густина постійна). При збільшенні довжини або густини збільшується маса струни, яка прагне знизити частоту; при цьому також збільшується натягнення, що повинне викликати підвищення частоти. Ці два чинники компенсують один одного.
і не залежать від довжини струни і її густини (до тих пір, поки густина постійна). При збільшенні довжини або густини збільшується маса струни, яка прагне знизити частоту; при цьому також збільшується натягнення, що повинне викликати підвищення частоти. Ці два чинники компенсують один одного.
Дата добавления: 2016-05-05; просмотров: 606;
