Вплив параметрів відновлення нерезервованих об’єктів на їх функційну безпечність

Для визначення показників функційної безпечності використовують методику згідно з п. 2.3.2 та складають граф безпечності (рис. 6.1).

Для порівняння параметрів відновлення і відмов об’єкта вводять додатковий показник – індекс відновлення безпечної роботи об’єкта N_вб=m/l_н, який показує, в скільки разів інтенсивність відновлення більше, ніж інтенсивність небезпечних відмов об’єкта. Тоді інтенсивність відновлення дорівнює m=N_вбl_н.

Рис. 6.1. Граф безпечності нерезервованого об’єкта

Н рис. 6.1 позначено:

P_о (t), P₁(t) – відповідноймовірності перебування об’єкта у станах S₀ і S₁;

l_н, m=N_вбl_н – інтенсивності небезпечних відмов об’єкта і його відновлення.

При функціонуванні об’єкт може бути у таких станах:

S₀ – технічний засіб знаходиться у працездатному та безпечному стані з імовірністю P_о (t);

S₁ – технічний засіб знаходиться у непрацездатному та небезпечному стані з імовірністю P₁(t).

Імовірність безпечної роботи не залежить від показників відновлення, а залежить тільки від інтенсивності небезпечних відмов і тривалості експлуатації

Імовірність та інтенсивність небезпечних відмов, середній наробіток до небезпечної відмови та щільність розподілу наробітку до небезпечної роботи визначають за формулами взаємозв'язку (5.12) - (5.14) і (5.30) і вони також не залежать від показників відновлення.

Імовірність безпечної роботи об’єкта не дорівнює ймовірності перебування його в небезпечному стані S₀, яка є функцією готовності до безпечної роботи К_б(t) і залежить як від інтенсивності небезпечних відмов і тривалості експлуатації об’єкта, так і від показників його відновлення. Коефіцієнт готовності до безпечної роботи об’єкта дорівнює

Для визначення функції К_б(t) складають диференціальні рівняння Колмогорова

(6.3)

Після заміни P₁(t)=1 – P₀(t) у першому рівнянні воно має вигляд

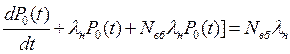. (6.4)

Використовуючи пряме перетворення Лапласа з урахуванням нульових початкових умов P(t=0)=1; P₁(t=0)=0, послідовно одержують

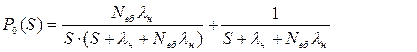
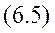
Рівняння (6.4) подають у вигляді суми (а = 0; b = l_н+N_вбl_н):

P₀(s) = 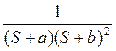+ (6.6)

Використовуючи обернене перетворення Лапласа для цієї функції, одержують її оригінал

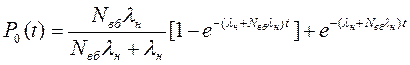(6.7)

Після введення останнього доданка в дужки й множення його на дріб 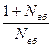оригінал функції готовності до безпечної роботи об’єкта буде мати вигляд

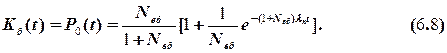
Коефіцієнт готовності до безпечної роботи об’єкта дорівнює

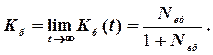(6.9)

При експоненціальних законах розподілу небезпечних відмов і тривалості відновлення об’єкта (при )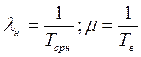

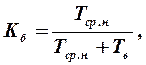(6.10)

де Т_ср.н – середній наробіток об’єкта до небезпечної відмови;

Т_в – середня тривалість відновлення об’єкта після

виникнення небезпечної відмови.

Функція готовності, коефіцієнт готовності до безпечної роботи та ймовірність безпечної роботи об’єкта подані на рис.6.2.

Рис. 6.2. Графіки функцій готовності та імовірності безпечної роботи об’єкта

Мінімальне значення

При великих значеннях N_вб можна приблизно вважати К_б(t)=К_б. Відносний час перебування системи в безпечному та небезпечному станах:

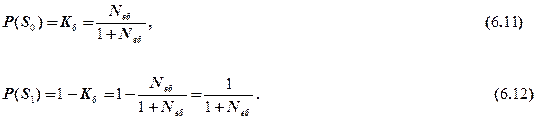
Графік залежності К_б=f(N_вб) наведений на рис. 6.3.

Рис.6.3. Графік залежності коефіцієнта безпечності від індексу відновлення об’єкта

Відношення ймовірностей перебування системи в безпечному й небезпечному станах дорівнює індексу відновлення

У технічних засобах без резервування прискорення відновлення призводить тільки до збільшення їхньої готовності до безпечної роботи. Зміна параметрів відновлення не змінює основні показники функційної безпечності таких об’єктів.