Вплив параметрів відновлення нерезервованих об’єктів на їх безвідмовність

При функціонуванні об’єкт може бути у таких станах:

S₀ – технічний засіб знаходиться у працездатному стані з імовірністю P_о (t);

S₁ – технічний засіб знаходиться у непрацездатному стані з імовірністю P₁(t).

Граф безвідмовності схожий на граф безпечності, має дві вершини та дві інтенсивності переходу (інтенсивність відмов і інтенсивність відновлення з працездатного стану). Тому результати розрахунку будуть схожими, тільки в них замість показників функційної безпечності будуть показники безвідмовності (відповідні індекси при показниках безвідмовності).

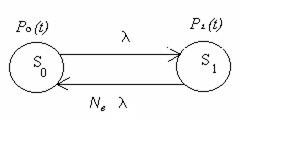
Рис. 6.4. Граф безвідмовності відновного об’єкта без резервування

Імовірність безвідмовної роботи об’єкта не залежить від показників відновлення, а залежить тільки від інтенсивності відмов і тривалості експлуатації

Імовірність та інтенсивність відмов, середній наробіток до відмови та щільність розподілу наробітку до відмови визначають за формулами взаємозв'язку (2.5), (2.14) і (2.18) і вони також не залежать від показників відновлення.

Імовірність безвідмовної роботи об’єкта не дорівнює ймовірності перебування його в непрацездатному стані S₀, яка є функцією готовності К_г(t) і залежить як від інтенсивності відмов і тривалості експлуатації об’єкта, так і від показників його відновлення.

Після складання диференційних рівнянь та їх розв’язання (подібно до визначення коефіцієнта безпечності) коефіцієнт готовності об’єкта дорівнює

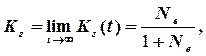(6.15)

де N_в – індекс відновлення, який показує, в скільки разів інтенсивність відновлення більше, ніж інтенсивність відмов об’єкта. N_в=m/l, Тоді інтенсивність відновлення дорівнює m=N_вl .

При експоненціальних законах розподілу небезпечних відмов і тривалості відновлення об’єкта (при )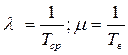

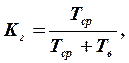(6.16)

де Т_ср – середній наробіток об’єкта до відмови;

Т_в – середня тривалість відновлення об’єкта після виникнення відмови.

У технічних засобах без резервування прискорення відновлення призводить тільки до збільшення їхньої готовності (що призводить, наприклад, до підвищення пропускної спроможності поїздів). Зміна параметрів відновлення не змінює показники безвідмовності таких об’єктів.

6.3. Розрахунок функційної безпечності відновлюваних технічних засобів у разі використання навантажувального і ненавантажувального дублювання

До мінімально можливих резервованих структур технічних засобів належать, у першу чергу, структури з навантажувальним і ненавантажувальним дублюванням (двоканальні структури). При використанні ненавантажувального дублювання необхідно враховувати зауваження, які наведено у п.п. 2.6, 2.7.

6.3.1. Розрахунок функційної безпечності відновлюваних технічних засобів у разі використання навантажувального дублювання з розв’язувальним елементом ”і”

Рис. 6.5. Розрахунково–логічна схема й граф безпечності відновного об’єкта при навантажувальному дублюванні

Небезпечна відмова системи настає тоді, коли відбудеться небезпечна відмова кожного з каналів резервування.

Імовірність небезпечної відмови дорівнює ймовірності перебування об’єкта у стані S₂:

Q_н (t)= P₂ (t).

Імовірність безпечної роботи дорівнює сумі ймовірностей перебування об’єкта у станах S₀ і S₁:

Р_б (t)=P₀(t)+ P₁(t).

Для визначення ймовірностей P₀(t), P₁(t) і P₂(t) складають систему диференційних рівнянь Колмогорова, яка з урахуванням співвідношення N_вб=m/l_н має вигляд

(6.17)

Після прямого перетворення Лапласа, з урахуванням нульових початкових умов: Р₀ (t=0)=1, P₁(t=0)= Р₂(t=0)=0, одержують

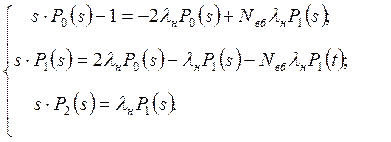(6.18)

Спочатку виконують перетворення першого рівняння системи (6.18)

P₀(s)[s+2l_н]= N_вбl_н P₁(s)+1;

P₀(s) = 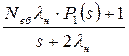. (6.19)

Підставляючи отриманий вираз у друге рівняння системи (6.18), одержують

.

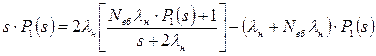Звідси

;

;

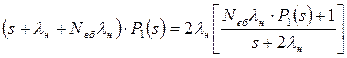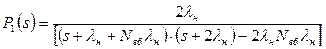. (6.20)

Після заміни в третьому рівнянні системи (6.15) зображення Р₁(s) на вираз (6.17) воно матиме вигляд

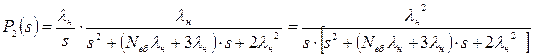. (6.21)

Далі позначають через S₁, S₂ корені квадратного рівняння знаменника P₂(s), які визначають у такий спосіб:

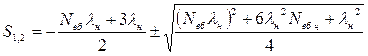
або

;

.

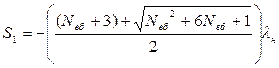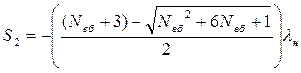З урахуванням уведених позначень вираз (6.18) буде мати вигляд

.

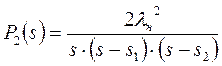Після використання оберненого перетворення Лапласа для рівняння P₂(s) одержують формулу для визначення ймовірності небезпечної відмови об’єкта

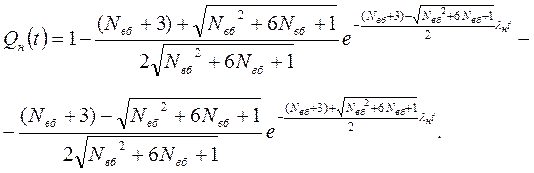(6.22)

Звідси одержують імовірність безпечної роботи об’єкта:

Після перетворення першого показника ступеня (при l_нt)шляхом помноження та ділення на однаковий сполучений доданок отримаємо

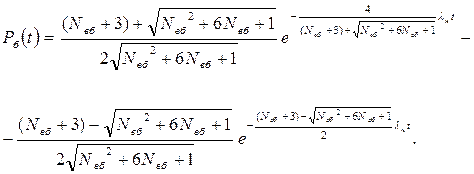(6.23)

Для більшості практичних випадків (при N_вб > 100), коли

імовірність безпечної роботи дорівнює

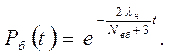(6.24)

Для визначення середнього наробітку до небезпечної відмови використовують рівняння ймовірності безпечної роботи

Р_б (t)=1 – P₂(t). (6.25)

Після прямого перетворення Лапласа рівняння (6.25) одержують

. (6.26)

З урахуванням приведення виразу (6.23) до загального знаменника зображення функції безпеки буде мати вигляд

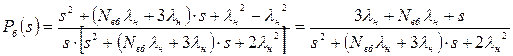. (6.27)

Середній наробіток до небезпечної відмови визначають з урахуванням формули (2.35)

. (6.28)

Після заміни в рівнянні (6.28) зображення ймовірності безпечної роботи на вираз (6.27) і проведення відповідних перетворень, отримують спрощену формулу для визначення середнього наробітку до небезпечної відмови:

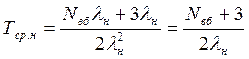(6.29)

або, з урахуванням уведення індексу відновлення безпечної роботи об’єкта N_вб=m/l_н = Т_ср.н/ Т_вб, одержують

(6.30)

де - Т_ср.нj - середній наробіток до небезпечної відмови одного каналу резервування.

При великих значеннях індексу N_вб (N_вб > 200) збільшення середнього наробітку до небезпечної відмови при введенні навантажувального дублювання залежить практично тільки від співвідношення інтенсивності відновлення та інтенсивності небезпечних відмов каналів резервування (індексу відновлення N_вб )

. (6.31)

Для цього випадку використовують також рівноцінну формулу

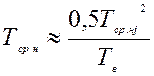. (6.32)

Для визначення коефіцієнта безпеки К_б використовують граф стану об’єкта (рис. 6.4), у якому додається ребро графа S₂–S₁. При відсутності відновлення, у випадку перебування системи в стані S₂, коефіцієнт безпеки К_б = 0. Це обумовлено тим, що коли є навіть мінімальна ймовірність переходу системи в стан небезпечної відмови, час перебування системи в цьому стані без відновлення буде дорівнювати нескінченності.

Коефіцієнт готовності об’єкта до безпечної роботи визначається в сталому режимі його роботи, тому систему диференційних рівнянь перетворюють у систему алгебраїчних рівнянь

(6.33)

Розв’язання системи (6.33) виконують з урахуванням додаткової умови

Р₀+Р₁+Р₂=1. (6.34)

З першого та третього рівнянь системи (6.30) отримаємо:

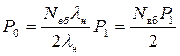; (6.35)

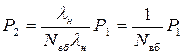; (6.36)

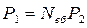. (6.37)

Підставляючи вирази (6.35)–(6.37) у рівняння (6.34) і, розв’язуючи його, одержують

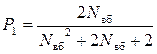. (6.38)

З урахуванням виразів (6.35) і (6.36)

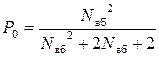; (6.39)

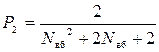. (6.40)

Коефіцієнт готовності до безпечної роботи об’єкта визначається сумою ймовірностей перебування системи в безпечних станах (S₀,, S₁)

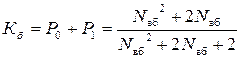. (6.41)

Коефіцієнт готовності до безпечної роботи об’єкта з навантажувальним дублюванням залежить тільки від індексу відновлення каналів резервування і підвищується при його збільшенні.

6.3.2. Розрахунок безвідмовності відновлюваних технічних засобів у разі використання навантажувального дублювання з розв’язувальним елементом ”і”

Граф безвідмовності у разі використання навантажувального дублювання з розв’язувальним елементом ”і” для експоненціального закону розподілу відмов (l= const) наведено на рис. 6.6.

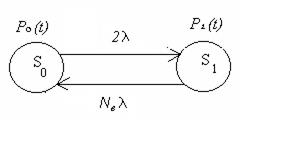
Рис. 6.6. Граф безвідмовності у разі використання навантажувального дублювання з розв’язувальним елементом ”і”

Захисна відмова системи настає тоді, коли відбудеться відмова будь-якого з двох каналів резервування, тому усі показники її безвідмовності зменшуються у порівнянні з одноканальною структурою.

Імовірність безвідмовної роботи системи дорівнює

Середній наробіток до відмови зменшується в 2 рази у порівнянні з одноканальною структурою.

У разі використання такої структури прискорення відновлення:

- не змінює показники безвідмовності таких об’єктів;

- призводить до збільшення готовності об’єктів, але у порівнянні з одноканальною структурою готовність зменшується з підвищенням індексу відновлення (при великих значеннях Nв у 2 рази).

Підвищення кількості каналів резервування об’єктів у разі прискорення (як і зменшення) тривалості відновлення не змінює показники безвідмовності, але у разі однакової тривалості відновлення зменшує готовність їх до працездатного стану.

6.3.3 Розрахунок функційної безпечності відновлюваних технічних засобів у разі використання ненавантажувального дублювання

Рис. 6.7. Розрахунково–логічна схема й граф безпечності об’єкта при ненавантажувальному дублюванні

Небезпечна відмова системи настає тоді, коли в процесі формування небезпечної відмови основного об’єкта виникне переключення його на резерв і після цього він небезпечно відмовить. Для визначення показників функційної безпечності складають систему диференційних рівнянь Колмогорова

(6.43)

Після прямого перетворення Лапласа, з урахуванням нульових початкових умов Р₀(0)=1, Р₁(0)= Р₂(0)=0, одержують

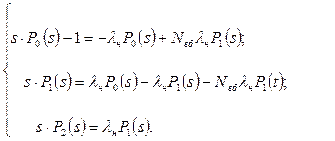(6.44)

Розв’язання першого рівняння системи (6.44) призводить до такого результату:

P₀(s) = 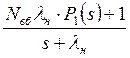. (6.45)

Підставляючи отриманий вираз у друге рівняння системи (6.44), послідовно одержують

;

;

;

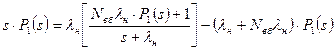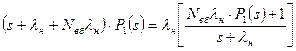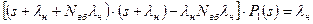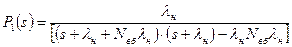. (6.46)

Після перетворення третього рівняння системи (6.44) та заміни в ньому рівняння (6.46) одержують

; (6.47)

. (6.48)

Для знаходження оригіналу функції (6.44) через S₁, S₂ позначають корені квадратного рівняння її знаменника, які визначають у такий спосіб:

, (6.49)

або

;

.

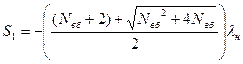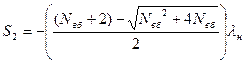Тоді

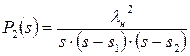. (6.50)

Використання оберненого перетворення Лапласа дозволяє визначити оригінал функції (6.50) і відповідно ймовірність небезпечної відмови об’єкта з ненавантажувальним дублюванням

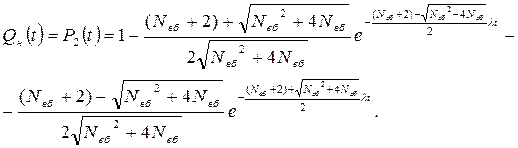(6.51)

Загальну ймовірність безпечної роботи об’єкта визначають за формулою

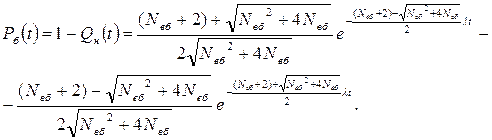(6.52)

Після перетворення першого показника ступеня (при lt)шляхом помноження та ділення на однаковий сполучений доданок отримаємо

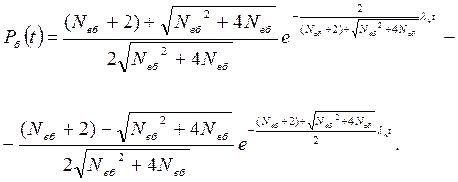(6.53)

Для більшості практичних випадків (при N_вб > 100), коли

імовірність безпечної роботи дорівнює

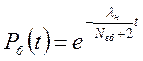. (6.54)

Для визначення середнього наробітку до небезпечної відмови використовують таке співвідношення:

.

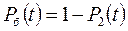Використовуючи пряме перетворення Лапласа, послідовно одержують

;

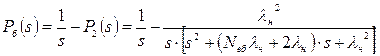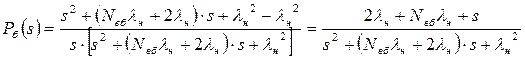. (6.55)

Середній наробіток до небезпечної відмови визначають з урахуванням формули (2.35)

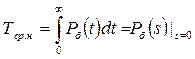. (6.56)

Після перетворень одержують

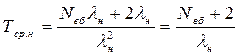(6.57)

З урахуванням співвідношення Т_ср.н1=1/l_н

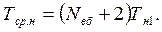(6.58)

При великих значеннях N_в (N_в >100) уведення ненавантажувального резервування прямо пропорційне індексу відновлення N_вб

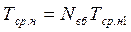. (6.59)

Для розрахунку використовують рівноцінну формулу

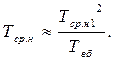(6.60)

Збільшення середнього наробітку до небезпечної відмови об’єкта при використанні ненавантажувального дублювання, у порівнянні з навантажувальним дублюванням, визначають таким чином:

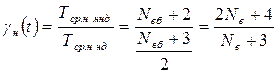. (6.61)

Значення функції g_н(t) змінюються в діапазоні від g_н(t)=1,33 (при N_в®0) до 2 (при N_вб ® ¥).

При великих значеннях N_вб (N_вб >50) підвищення середнього наробітку до небезпечної відмови при ненавантажувальному дублюванні практично у два рази більше, ніж при навантажувальному дублюванні.

Для визначення коефіцієнта готовності до безпечної роботи об’єкта використовують граф стану системи (рис. 6.6), у який додається ребро графа S₂ – S₁.

Коефіцієнт готовності до безпечної роботи об’єкта визначається в сталому режимі його роботи, тому систему диференційних рівнянь перетворюють у систему алгебраїчних рівнянь

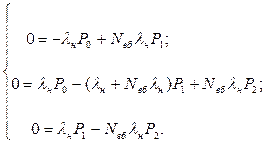(6.62)

Додаткове рівняння

Р₀+Р₁+Р₂=1. (6.63)

З першого та третього рівнянь системи (6.58) одержують

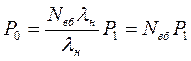; (6.64)

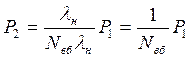. (6.65)

Після підстановки виразів (6.64) і (6.65) у рівняння (6.63) одержують

.

Звідси одержують імовірність перебування об’єкта у стані S₁ (безпечному та непрацездатному стані):

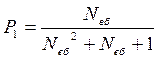. (6.66)

З урахуванням виразів (6.64) і (6.65) імовірності перебування об’єкта у станах S₀ (безпечному та працездатному стані) та S₂ (небезпечному стані) у сталому режимі дорівнюють

; (6.67)

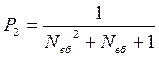. (6.68)

Коефіцієнт готовності до безпечної роботи об’єкта визначають шляхом додавання ймовірностей перебування системи в безпечних станах (S₀, S₁):

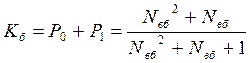. (6.69)

Коефіцієнт готовності до безпечної роботи об’єкта також залежить тільки від індексу відновлення та підвищується з його збільшенням.

У разі використання ненавантажувального дублювання об’єктів і прискорення їх відновлення суттєво підвищується як їх функційна безпечність, так і їх готовність до безпечної роботи. Підвищення кількості каналів резервування ще більше покращує ці показники.

6.3.4. Розрахунок безвідмовності відновлюваних технічних засобів у разі використання ненавантажувального дублювання

Граф безвідмовності має вигляд, що подібний графу безпечності об’єкта з ненавантажувальним дублюванням, тільки в ньому замість інтенсивності небезпечних відмов треба використовувати інтенсивність відмов, а замість індексу відновлення з небезпечного стану – індекс відновлення з працездатного стану об’єкта.

Показники безвідмовності для такої структури розраховуються за формулами п. 6.3.3, тільки в них замість показників функційної безпечності використовують відповідні показники безвідмовності.

У разі використання ненавантажувального дублювання об’єктів і прискорення їх відновлення суттєво підвищується як їх безвідмовність, так і їх готовність. Підвищення кількості каналів резервування ще покращує ці показники.