Многоступенчатая выборка
Отметим, что в реальной практике чаще всего применяется многоступенчатая выборка, построенная с применением проя цедуры поэтапного отбора объектов опроса. При этом совокупч ность объектов, отобранных на предыдущем этапе (ступени)
становится исходной для отбора на следующем. Соответственно различают единицы отбора первой ступени (первичные единицы), единицы отбора второй ступени (вторичные единицы) и т.д. Объекты самой нижней ступени, с которых ведется непосредственный сбор информации, называются единицами наблюдения.
Приведем пример многоступенчатой выборки, которую мы рассчитывали в ходе одного из маркетинговых омнибусных26 исследований, проводившихся при нашем участии в ряде крупных регионов России в 1995 г. одним из столичных маркетинговых центров. Для Нижнего Новгорода объем выборки был задан в 900 человек. В качестве единиц отбора первой ступени были определены три городских района из восьми с объемом выборки 300 респондентов по каждому. Здесь, как и на следующей ступени, был использован метод типичных представителей. Определив среднюю численность населения одного района, мы остановили свой выбор на трех районах — Канавинском, Советском и Нижегородском, численность населения которых в наименьшей степени отклонялась от этого среднего значения. За основу выборки на второй ступени были взяты списки избирателей (большинство из которых выступают самостоятельными экономическими агентами рынка в качестве покупателей). Здесь в качестве единиц отбора второй ступени были определены по три избирательных участка. Также были рассчитаны средние размеры каждого из участков и отобраны те из них, где численность избирателей в наименьшей степени отклонялась от средней. На третьей ступени за основу выборки принимался список избирателей каждого участка. Было определено, что на каждом участке предстоит опросить по 100 человек (я(.= 100). На этом последнем этапе для окончательного отбора единиц наблюдения применялся метод систематической выборки. Определив шаг выборки, мы получили списки респондентов с домашними адресами. Поскольку во всех районах имелись электронные версии списков избирателей, вся процедура заняла менее одного дня.
Отметим, что и в приведенном выше примере опроса избирателей в ходе избирательной кампании фактически использо-
валась многоступенчатая выборка. На первой ступени была произведена квотная выборка по параметрам пола и возраста, а на втором рассчитана территориальная квота — по параметрам численности каждого избирательного округа. Затем была опять просчитана половозрастная квота для каждой из первичных единиц отбора (округов). Кроме того, была задана половозрастная квота для каждого из тридцати анкетеров по отдельным
участкам опроса.
К многоступенчатому отбору прибегают в тех случаях, когда генеральная совокупность имеет настолько большой объем, что простой случайный или систематический отбор элементов привел бы к чрезмерному распылению выборки по всей территории. Попросту говоря, такой метод применяют в тех случаях, когда изучают достаточно большие группы людей или крупные общности, скажем регион или город.
В многоступенчатой выборке каждая единица отбора представляет собой гнездо единиц более низкого уровня, поэтому многоступенчатый отбор позволяет локализовать выборку в меньшем числе точек. Большой массив социолог начинает последователь-но сужать, проходя множество ступеней, доводя большую сово-купность до такой малой величины, что ее можно охватить одним взглядом, а если это территория, то обойти ногами. Город делит-ся на районы, те — на кварталы, затем выделяют избирательные участки, а в них отбирают домохозяйства.
Многоступенчатая выборка поначалу напоминает огромную воронку, поскольку широкое горлышко (огромную совокупность респондентов или объектов) через ряд процедур сводят к узкой горловине, с которой социолог в конечном итоге и имеет дело.
Однако то, что облегчает его жизнь на этапе составления вы-борки, сильно затрудняет его существование на конечной фазе, когда он подсчитывает величину ошибки и думает, на какую ге-неральную совокупность он может распространить свои выводы
При этом не стоит забывать: чем больше ступеней в многоступенчатом oт боре, тем больше ошибка выборки. В любом случае при многоступенчатом отборе ошибка всегда больше, чем при простом случайном. И еще: на каж-дой ступени все равно применяется случайный отбор.
Такая вот странная диалектика у нас получается: число оши-бок на каждой ступеньке возрастает, они накапливаются с каж-дым шагом и разрастаются к концу исследования до неуправляе-мых размеров. Вместо обратной пирамиды, т.е. воронки, мы по-лучили теперь прямую пирамиду (рис. 2.4).
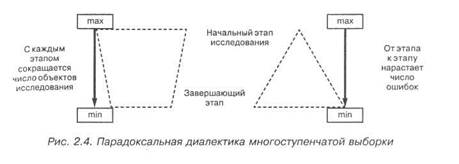
Специалисты об этом явлении говорят так: на каждой ступени процессу независимого извлечения выборки сопутствует своя выборочная ошибка. Отдельные ошибки складываются в общую ошибку многоступенчатой выборки. Таким образом, увеличение количества ступеней, с одной стороны, приводит к сокращению базовых точек опроса и, следовательно, к экономии людских и материальных ресурсов, с другой — к уменьшению точности выборочных оценок27.
2.7. Идеальные и реальные совокупности
Обследуемый объект — выборочная совокупность — представляет собой явление, таящее в себе массу противоречий и подводных камней. Социологу следует помнить, что этот объект не существует в реальности — он сконструирован процедурой операционализации переменных, методикой выборки респондентов, условиями наблюдения, проведения интервью или эксперимента.
«Действительно, выборочная совокупность, с которой непосредственно «снимаются» данные, порождается процедурой, но в то же время она растворена в большой совокупности, которую представляет или репрезентирует с разной степенью точности и надежности. Социологические заключения относятся не к обследованным на прошлой неделе респондентам, а к идеализированным объектам: «старшим поколениям», «молодежи» и т.д.»28.
В идеале представляется, что из генеральной совокупности делается правильная выборка и опрашиваются только те, кто в нее попал. Однако подобная идеальная ситуация происходит далеко
не всегда. Социолог правильно определил генеральную совокупность, сделал правильную выборку, но при обходе домов и опросе респондентов возникли непредвиденные сложности и часть из них или выпала, или была заменена на других. В результате те, кто попал в выборку, и те, кто был реально опрошен, представляют разные совокупности людей. В итоге вместо одного объекта исследования мы получили целых два.
Предположим, что социолог интересуется мнением россиян накануне президентских выборов. Что входит в понятие «россияне»? Объем понятия «россияне» охватывает, по всей видимости, всех, кто является гражданином России и имеет право участвовать в президентских выборах. Назовем всех мыслимых россиян, соответствующих данному свойству, идеально планируемой генеральной совокупностью.Но на практике обследовать всех, кто охвачен теоретически сконструированным понятием «россияне», невозможно. «Среди россиян немало людей находится в тюрьмах, исправительно-трудовых учреждениях, в следственных изоляторах и иных труднодоступных для интервьюера местах. Эту группу придется «вычесть» из проектируемого объекта. «Вычесть» придется и многих пациентов психиатрических больниц, детей, часть престарелых. Вряд ли гражданскому социологу удастся обеспечить нормальные шансы на попадание в выборку и военнослужащим. Аналогичные проблемы сопровождают обследование читателей, избирателей, жителей малых городов, посетителей театров... Помимо заключенных, военнослужащих и больных, меньшую вероятность попасть в выборку имеют жители удаленных от транспор-тных коммуникаций сел, особенно если обследование производит-ся осенью; те, кого, как правило, нет дома, не склонны к разговорам с посторонними людьми и т.п. Бывает, что интервью- еры, пользуясь отсутствием контроля, пренебрегают точным ис-полнением своих обязанностей и опрашивают не тех, кого поло-жено опрашивать по инструкции, а тех, кого легче «достать».
Исключив из идеальной генеральной совокупности все труд- недоступные единицы наблюдения, мы получим более узкое по-нятие —реально получившуюся генеральную совокупность. В мето- дологической литературе первая получила также название концеп-туального объекта, а вторая — проектируемого.
Концептуальный объект — идеальный конструкт, обозначаю- щий рамки темы исследования. Проектируемый объект — сово-купность доступных исследователю единиц.
Итак, взвесив свои возможности и поняв, что всех, кто идеально подходит для нашей генеральной совокупности, мы опросить по разным обстоятельствам не сможем, мы получаем в итоге новую генеральную совокупность, из которой и должны исходить, проектируя свою выборку. Они могут различаться совсем незначительно (если труднодоступных единиц наблюдения мало) или очень значительно (если таковых много).
Поскольку два объекта расходятся, то следует заново переопределить генеральную совокупность. Старое определение: генеральная совокупность — это та совокупность, из которой предполагается производить выборку единиц. Новое определение: генеральная совокупность — это та совокупность, из которой производится выборка единиц. Чем они различаются? Старое определение не учитывает труднодоступность и возможные на практике ограничения, но указывает на теоретически возможный объем понятия, скажем «россияне». В теоретически сконструированной генеральной совокупности, согласно официальной статистике, например, 49% мужчин и 51% женщин. Но когда социолог отбросил все труднодоступные единицы наблюдения и дал новое определение, приближенное к реальности обследования, у него получилось, к примеру, 43% мужчин и 57% женщин (уменьшение количества мужчин могло произойти за счет того, что, скажем, опросить военных и заключенных накануне президентских выборов практически невозможно или нереально).
Из какой генеральной совокупности — теоретически мыслимой или реально существующей — должен исходить социолог? Видимо, из второй. А с какой генеральной совокупностью он должен сравнивать выборочную после полевого исследования и устанавливать меру отклонения, т.е. определять репрезентативность? Обязательно со второй. Но часто об этом забывают и сравнение происходит с первой совокупностью, хотя выборка производилась из второй.
Однако трудности встречаются, как мы уже выяснили, не только на пути конструирования генеральной совокупности. Не меньше, если не больше, их и на пути конструирования, а затем и обследования выборочной совокупности. Выше они были сгруппированы в два типа ошибок выборки — случайные и систематические. Для неопытного полевого социолога они могут стать мощнейшим фактором возмущения и причиной серьезных погрешностей.
В результате наложения двух типов ошибок происходит не меньшее, если не большее, чем в случае с генеральной совокупностью, отклонение идеально запроектированной выборки от ре-120
ально получившейся. Отклонение реальной выборки от проектируемой можно наглядно изобразить на схеме.
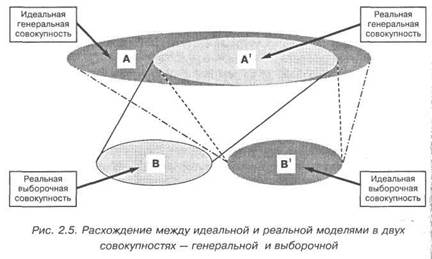
На рис. 2.5 сплошной линией обозначена связь двух реаль-ных выборок: А'ЮВ; она символизирует то, что получилось в эм-лирическом исследовании в действительности. Хотя, конечно же, социологу мечталось о другом. В идеале он желал бы получить связь АЮВ1, т.е. чтобы из идеально сконструированной и мак-симально широкой генеральной совокупности у него получилась максимально полная и репрезентативная выборка. Но позже, ког-да он осознал невозможность получения идеальной генсовокуп-ности, он устремился ко второму варианту — получить связь А'ЮВ1, т.е. из ограниченной генсовокупности получить макси-мально полную выборку. На самом же деле, преодолев многочис-ленные трудности и наделав множество ошибок (случайных и си-стематических), социолог получил самый худший вариант,а именно А'ЮВ.
Для сокращения разрыва между идеальной (проектируемой) и реальной (получившейся) выборками, приведения в соответствие замысла и действительности социологи разработали множество до-вольно эффективных приемов: контроль выборки (увеличение удельного веса недостающих групп и уменьшение избыточных), ремонт выборки (замена труднодоступных респондентов анало-гичными по задаваемым признакам индивидами), контроль запол-нения вопросников и др. С их помощью реальный массив подго-няется под проектируемый.
2.8. Расчет объема выборки30
Из всех вопросов, которые задают сотрудникам знаменитого Института опросов общественного мнения Гэллапа, самым популярным является такой: как вы можете, проинтервьюировав 1000 человек, судить о том, что думают 250 млн американцев?
Для ответа на этот вопрос нужно упомянуть не только высокую квалификацию и огромный практический опыт сотрудников, но и использование ими статистики и математики. Если методы опроса не основаны на науке, результаты могут ввести вас в заблуждение.
В статистике приняты следующие разграничения объемов выборки. Объем выборки, достаточный для взаимопогашения случайностей и получения статистических характеристик закономерного характера, равен 30. Выборка такого объема называется малой. Характер распределения значений признака в малых выборках приближается к нормальному с ростом числа испытаний. Минимальный объем выборки, позволяющий получить средние значения признака с указанием доверительных вероятностей, равен 5. Выборки такого объема называются сверхмалыми. Распределение значений признака в таких выборках характеризуется распределением Стьюдента. Но чаще всего в социологии имеют дело с гораздо большим объемом выборки.
При планировании выборочного обследования наступает момент, когда нужно решить, сколько человек опрашивать, т.е. каким должен быть объем выборки. Это решение чрезвычайно важно, поскольку слишком большая выборка потребует излишних затрат, а слишком маленькая понизит качество результатов.
Объем выборки — общее число единиц наблюдения, включенных в выборочную совокупность.
Поскольку выборочная совокупность — это часть генеральной совокупности, отобранная с помощью специальных методов, — важно, чтобы эта часть не искажала представления о целом, т.е. репрезентировала его. Социологов, часто проводящих эмпирические исследования, постоянно волнует вопрос о том, как много надо опрашивать человек, чтобы получить достоверную информацию? Институт Гэллапа в США проводит регулярные опросы по национальной выборке объ
1,5%). Центр «Социо-Экспресо Института социологии РАН проводит исследования на выборке объемом в 2 тыс. человек, при этом ошибка выборки не превышает 3%31.
Специалисты считают, что наилучшая выборка — не обязательно большая. Конечно, чем больше объем выборки, тем выше точность ее результатов. Однако даже огромная выборка не гарантирует успеха, если генеральная совокупность «плохо перемешана», т.е. является неоднородной. Однородной считается такая совокупи ность, в которой контролируемый признак распределен равномер-но, не образует пустот или сгущений. В этом случае, опросив нескольких человек, можно получить точную информацию о распределении этого признака в генеральной совокупности.
Таким образом, на репрезентативность данных влияют не количественные характеристики выборочной совокупности (ее объем), а качественные характеристики генеральной совокупнос-ти — степень ее однородности.
В социологии еще не придумано единой и четкой формулы, используя которую можно рассчитать оптимальный объем выборочной совокупности, — такой формулы просто не существует в природе. И объясняется это весьма просто. Дело в том, что опре-деление объема выборочной совокупности — проблема не столько статистическая, сколько содержательная. Иными словами, объем выборочной совокупности зависит от множества факторов, в том числе от целей и задач, теоретической модели, гипотез и методов исследования, степени однородности генеральной совокупности наконец, требующейся точности получаемой информации.
Надо всегда помнить, что каждый процент прироста точности ин-формации в исследовании приводит к резкому увеличению расходов на его проведение. Знаменитый институт Гэллапа, на протяжении многих десятилетий проводящий опросы в США, выявил, что при общенациональной выборке в 100 человек — ошибка выборки будет в пределах ±11%; 200 человек - ±8%; 400 - ±6%; 600 - ±5%; 750 — ±4%; 1000 - ±4%; 1500 - ±3%; 4000 человек - +2%. Именно поэто-му он проводит общенациональные опросы в США на выборке в 1500-2000 человек. Как видно, он предпочитает увеличение ошибки на 1% многократному увеличению стоимости исследования.
Практика показывает, что для многих социологов обоснование объема выборки является камнем преткновения, несмотря на зна- чительное количество литературы, посвященной выборочным
методам и, в частности, расчету объема выборки. Причин несколько: 1) дефицит специальной литературы на периферии; 2) нехватка времени для самообразования; 3) неумение пользоваться математическим аппаратом. В связи с этим возникает необходимость без сложных математических формул изложить стратегию и тактику обоснования объема выборки.
Процедура расчета объема выборки — цепь бесконечных компромиссов между стремлением к точности и ограниченностью ресурсов, дефицитом времени и неполнотой сведений об изучаемом явлении. Вместе с тем это наука и искусство, познание которых доступно каждому человеку. Однако для этого нужно знать стратегии расчета объема выборки (предварительного расчета, последовательной и комбинированной стратегии), а также факторы, влияющие на объем выборки (объем генеральной совокупности, варьирование ответов респондентов, точность оценивания, характер предполагаемого распределения ответов, метод исследования, процедура обработки).
Стратегия предварительного расчетасостоит в том, что объем выборки определяется до проведения основного исследования. В наиболее простом случае можно воспользоваться уже наработанным опытом, например, института Гэллапа, где используется объем выборки приблизительно в 1500—2000 человек. Для среднестатистического отечественного исследования объема выборки — примерно 400—600 человек.
Для расчета объема случайной выборки надо знать желаемую точность оценивания, величину риска получаемого ответа и степень изменчивости ответа. Традиционно точность оценивания принимают за 5%, а величину риска — за 0,95. Иными словами, если по данным выборочного исследования 60% опрошенных удовлетворены работой, то можно утверждать, что в генеральной совокупности доля удовлетворенных составит от 55 до 65% в 95% случаев, а в 5% случаев такая доля может выйти за этот интервал. Если исходить из 5%-ной точности и величины риска в 0,95, объем выборки будет следующим (табл. 2.4).
Таблица 2.4 Зависимость объема выборки от объема генеральной совокупности
| Объем генеральной совокупности | Бесконечная | ||||||||
| Объем выборки |
Результаты, приведенные в табл. 2.4, свидетельствуют против Распространенного заблуждения, будто бы объем выборки — же-
стко фиксированный процент от генеральной совокупности, рав-ный 10. На самом же деле эта величина — не постоянная, а пере-менная, изменяющаяся в конкретных условиях. Объем выборки зависит также от того, какие вопросы используются в анкете. Цифры в табл. 2.4 действительны только для одного случая — ког-да речь идет о дихотомическом вопросе, у которого максималь- ный разброс ответов — 50 на 50%. Не имея предварительной ин-формации о разбросе оценок, социолог как бы заранее страхуется и считает, что этот разброс составит 50 на 50%. Если же такая информация имеется, то объем выборки будет следующим..
Таблица 2.5 Зависимость объема выборки от распределения дихотомического ответа
| Распределение ответов, % | |||||
| Объем выборки |
В табл. 2.5 показано распределение ответов на качественные вопросы. Расчет объема выборки для количественных вопросов, включающих вопросы типа «возраст» и «заработная плата», строится исходя из коэффициента вариации (табл. 2.6), который по-казывает, какой процент составляет среднее квадратическое откло-нение от средней арифметической, и позволяет сравнивать межч-ду собой (по степени варьирования) любые признаки.
Таблица 2.6
Зависимость объема выборки от коэффициента вариации
| Коэффициент вариации, % | 110 I 120 | ||||||||||
| Объем выборки | 1860|2213 |
Если изучаются условия труда, взаимоотношения в коллективе, заработная плата и т.д. с помощью пятичленной шкалы,то коэффициент вариации изменяется здесь от 27 до 62%, а при ис-пользовании семичленной — от 78 до 113%. Стало быть, чем длиннее шкала, тем выше коэффициент вариации и больше должен быть объем выборки. Если социолог хочет обойтись неболь-шой выборкой, то и вопросы должен формулировать проще. Иногда думают, что чем длиннее шкала, тем точнее измерение Но преимущества семибалльных шкал над пятибалльными не доказаны.
Среди социологов распространено мнение, согласно которому чем больше объем выборки, тем точнее результат, и это заставля-ет их непомерно увеличивать количество опрошенных. В реаль-
ности дело обстоит иначе: табл. 2.7, составленная по данным Института Гэллапа, показывает зависимость между объемом выборки и точностью оценивания в процентах. Из нее следует, что с увеличением объема выборки точность возрастает, но до определенного порога. Уже при 600 опрошенных достигается желанный для всех 5%-ный уровень точности. Стало быть, 600 человек — приемлемый объем выборки.
Между цифрами 400 и 600 человек противоречия нет. В первом случае объем выборки рассчитывался, исходя из положения о нормальном распределении ответов респондентов, а во втором — из практики. Расхождение между теорией и практикой обусловлено тем, что в реальной ситуации распределение оценок отличается от нормального, поэтому объем выборки надо рассчитывать с учетом именно этого обстоятельства; наиболее эффективным способом уменьшения объема выборки является снижение коэффициента вариации оценок.
Таблица 2.7 Зависимость между объемом выборки иточностью оценивания
| Количество интервью | Точность оценивания,% |
| ±11 | |
| ±8 | |
| ±6 | |
| ±5 | |
| ±4 | |
| ±4 | |
| ±3 | |
| ±2 |
При расчете объема выборки социологи часто совершают такую ошибку: рассчитав по существующим формулам необходимый объем выборки в целом для совокупности, в дальнейшем пропорционально размещают его по отдельным подразделениям выборки, например по цехам, предприятиям, районам, городам, типам семей. После чего на этапе обработки данных — анализируют уже сами различия между подразделениями. Однако правильнее вычислить объем выборки отдельно для каждого подразделения, а затем суммировать отдельные объемы. Допустим, расчеты объема выборки по трем цехам (с учетом размерности шкалы, численности работающих, характера предполагаемого распределения оценок) позволили установить, что в первом цехе необходимо спросить 384 человека, во втором — 222, а в третьем — 600. Тогда общий объем выборки составит 384 + 222 + 600 = 1206 человек
Если социологу необходимо опросить какую-либо катего- рию работников (допустим, водителей автобусов), о которой из- вестно лишь, что к ней принадлежит, например, десятый работник предприятия, и он решил спросить 139 водителей автобусов, а общий объем выборки для предприятия составит 1390 человек, т.е. иными словами, отбирая случайным образом 1390 респондентов на предприятии, мы в соответствии с теорией выборки надеемся выявить 139 человек интересующей нас специальности.
При расчете квотной выборки социологи часто произвольно определяют ее объем в 1000 человек, исходя из удобства вычисления квот. Но с таким же успехом можно взять любое другое круглое число. Более обоснованным является подход, при котором, объем квотной выборки рассчитывается как для случайной. Дру-гим вариантом расчета объема квотной выборки является исполь-зование теории малых выборок. Ее суть: если не ставится цель дать дифференцированный анализ по группам работников, то умножа-ют количество градаций вопросов, подлежащих изучению, на 25 (минимальный статистический значимый размер группы). Напри-мер, изучают три переменные: пол — две категории, возраст — две категории (до 30 лет и свыше 30 лет), удовлетворенность трудом — измеряется пятибалльной шкалой. Тогда необходимый объем вы- борки для данного примера составит 2x2x5x25 = 500 человек. Объем выборки увеличивается в 2,5 раза. Ясно, что с расширени- ем числа переменных и числа градаций объем выборки может стать катастрофически большим. Выход только один: детальная проработка исходной проблемы, которая позволит отбраковать лишние вопросы в анкете, оставив самые важные. Если в иссле-довании проверяется несколько гипотез, то объем выборки для проверки каждой гипотезы вычисляется отдельно. Таким образом, при использовании выборки количество вопросов в анкете и гипотез должно быть минимальным.
Итак, мы рассчитали требуемый объем выборки. Теперь, и только теперь необходимо проверить, совместима ли полученная величина с выделенными ресурсами. Типичная ошибка многих социологов-прикладников состоит в том, что при расчете объема выборки во главу угла ставятся наличные ресурсы или, хуже того, социолог пассивно принимает все условия, диктуемые заказчиком.. Это в корне неверно по нескольким причинам. Во-первых, расчет объема выборки позволяет глубже проникнуть в суть изучаемого предмета и специфику методов исследования, а значит, ар- гументированно требовать получения больших ресурсов или при-нять правильное решение о снижении объема выборки. Если администрация отказала в дополнительных ресурсах, а цели ис-
следования не позволяют сократить объем выборки (т.е. социолог не может принять решение администрации), то надо переходить к другой схеме исследования. Во-вторых, обоснованный расчет объема выборки показывает профессионализм социолога и заставляет заказчика относится к нему более уважительно.
Стратегия последовательного расчетаобъема выборки. При расчете объема выборки желательно знать разброс оценок и некоторые другие параметры. Однако они-то, как правило, неизвестны. Для того чтобы не допустить ошибки, лучше предположить, что они максимальны. Плата за наше незнание — разбухание объема выборки сверх необходимого и дополнительные финансовые и временные затраты (приходится опрашивать большее число людей). Для сохранения затрат применяется последовательная стратегия — объем выборки не рассчитывается заранее, а ставится в зависимость от конечных результатов исследования. Например, опрашивают 100 человек, затем устанавливают величину разброса оценок и уже в зависимости от этого рассчитывают необходимый объем выборки. Если оказывается, что 100 человек достаточно, то исследование заканчивается. В противном случае добирается необходимое количество респондентов, но не до бесконечности. Известен пример из практики Дж. Гэллапа, который в начале своей карьеры активно экспериментировал с объемами выборки. В 1936 г. американцам был задан вопрос: «Хотели бы вы возобновления закона о восстановлении национальной промышленности?» Выяснился странный парадокс: Дж. Гэллап вначале опросил 500 человек и замерил ошибку выборки, а затем последовательно наращивал число респондентов до 30 тыс. К своему сожалению, он обнаружил, что прибавление 29,5 тыс. опрошенных увеличило точность информации менее чем на 1%. Следовательно, опрос можно было прекращать уже при 500 опрошенных. Этот пример показывает, что, применяя последовательную стратегию, можно добиваться значительного снижения необходимого числа наблюдений по сравнению с предварительным расчетом объема выборки.
Однако стратегия последовательного расчета объема выборки приносит желаемый результат лишь в том случае, если социолог может производить необходимые расчеты в ходе самого опроса, например телефонного, с применением компьютерных систем. Социолог вводит ответы респондента в свой персональный компьютер, с него результаты сразу поступают на компьютер руководителя исследования, обрабатываются, и на экране дисплея выдается информация не только об одномерных частотах, распределенных по тому или иному вопросу, но и о требуемом объеме выборки..
Если существует опасность, что объем выборки может оказаться катастрофически большим, надо совместить оба вида стратегии — предварительную и последовательную, т.е. применить комбиниро- ванную стратегию. Рассчитывая выборку по предварительной стратегии, получаем верхние допустимые значения для последовательной стратегии или, иначе говоря, ту величину объема выборки, при достижении которой прекращается опрос по последователь- ной стратегии.
Наиболее обоснованный и корректный подход к определению объема выборки основан на расчете доверительных интервалов, в: основе которого лежит ряд базовых понятий математической статистики (вариация, среднее квадратическое отклонение, довери-тельный интервал, средняя квадратическая ошибка).
Для расчета необходимого размера выборки в количественном исследовании чаще всего используют два статистических поня-тия — доверительный интервал и доверительную вероятность. Доверительный интервал представляет собой заранее задаваемую вами погрешность выборки. Например, если вы задаете доверй-тельный интервал в 3% и конкретный ответ на конкретный воп-рос исследования составит 48%, это значит, что даже при прове- дении опроса всей генеральной совокупности реальное значение попадет в интервал между 45 (48-3) и 51% (48 + 3). Доверитель-ная вероятность показывает, насколько вы можете быть уверены в полученных результатах, в том, что характеристики выборки со-ответствуют характеристикам всей генеральной совокупности -иными словами, с какой вероятностью случайный ответ попадет в доверительный интервал. Обычно используют доверительную вероятность 95 и 99%. Чаще всего используется 95% — этого впол-не достаточно в подавляющем большинстве исследований. Если объединить доверительную вероятность и доверительный интер-вал, то можно сказать, что ответы на вопрос с 95%-ной вероятно-стью попадут в интервал между 45 и 51%.
Весьма полезна следующая приблизительная оценка надеж-ности результатов выборочного обследования. Повышенная на-дежность допускает ошибку выборки до 3%, обыкновенная — от 3 до 10% (доверительный интервал распределений на уровне 0,03-0,1), приближенная — от 10 до 20%, ориентировочная — от 20 до 40%, а прикидочная — более 40%33.
На основе этих понятий с учетом ряда предположений выводятся формулы расчета объема выборки, которые предполагают,
что репрезентативность гарантируется путем использования корректных вероятностных процедур формирования выборки.
В ряде случаев в качестве главного аргумента при определении объема выборки используется стоимость проведения обследования. Так, в бюджете маркетинговых исследований предусматриваются затраты на проведение определенных обследований, которые нельзя превышать, и очевидно, что ценность получаемой информации не принимается при этом в расчет. Однако в ряде случаев и малая выборка может дать достаточно точные результаты.
Исследовательская практика подсказывает следующее правило: объем выборки должен обеспечивать не менее 100 наблюдений для каждой первостепенной и не менее 20—50 наблюдений для каждой второстепенной классификационной составляющей. Первостепенные классификационные составляющие соответствуют наиболее критичным, а второстепенные — наименее критичным ячейкам перекрестной классификации, принятой в данном исследовании34. Теоретические расчеты и практика доказывают, что для получения достоверных данных о мнении и предпочтениях населения такого крупного города, как Санкт-Петербург, достаточно опросить 700—800 человек. Однако большинство опросов населения здесь проходят на выборках объемом до 1,5 тыс. человек.
2.9. Ошибка выборки
Как мы уже знаем, репрезентативность — свойство выборочной совокупности представлять характеристику генеральной. Если совпадения нет, говорят об ошибке репрезентативности — мере отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. Предположим, что средний ежемесячный семейный доход пенсионеров в генеральной совокупности составляет 2 тыс. руб., а в выборочной — 6 тыс. руб. Это означает, что социолог опрашивал только зажиточную часть пенсионеров, а в его исследование вкралась ошибка репрезентативности. Иными словами, ошибкой репрезентативности называется расхождение между двумя совокупностями — генеральной, на которую направлен теоретический интерес социолога и представление о свойствах которой он хочет получить в конечном итоге, 130
и выборочной, на которую направлен практический интерес социолога, которая выступает одновременно как объект обследования и средство получения информации о генеральной совокупности.
Наряду с термином «ошибка репрезентативности» в отечественной литературе можно встретить другой — «ошибка выборки». Иногда они употребляются как синонимы, а иногда «ошибка выборки» используется вместо «ошибки репрезентативности» как количественно более точное понятие.
Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.
На практике ошибка выборки определяется путем сравнения известных характеристик генеральной совокупности с выборочными средними. В социологии при обследованиях взрослого населения чаще всего используют данные переписей населения, текущего статистического учета, результаты предшествующих опросов. В качестве контрольных параметров обычно применяются социально-демографические признаки. Сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки иее уменьшение называется контролированием репрезентативности. Поскольку сравнение своих и чужих данных можно сделать по завершении исследования, такой способ контроля называется апостериорным, т.е. осуществляемым после опыта.
В опросах Института Дж. Гэллапа репрезентативность контролируется по имеющимся в национальных переписях данным о распределении населения по полу, возрасту, образованию, доходу, профессии, расовой принадлежности, месту проживания, величине населенного пункта. Всероссийский центр изучения общественного мнения (ВЦИОМ) использует для подобных целей такие показатели, как пол, возраст, образование, тип посе- ления, семейное положение, сфера занятости, должностной ста- туе респондента, которые заимствуются в Государственном комитете по статистике РФ. В том и другом случае генеральная совокупность известна. Ошибку выборки невозможно установить, если неизвестны значения переменной в выборочной и ге-неральной совокупностях.
Специалисты ВЦИОМ обеспечивают при анализе данных тщательный ремонт выборки, чтобы минимизировать отклонения, возникшие на этапе полевых работ. Особенно сильные смещения наблюдаются по параметрам пола и возраста. Объясняется это тем, что женщины и люди с высшим образованием больше времени
проводят дома и легче идут на контакт с интервьюером, т.е. являются легко достижимой группой по сравнению с мужчинами и людьми «необразованными»35.
Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.
Ошибки выборки подразделяются на два типа — случайные и систематические. Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности (табл. 2.8).
Таблица 2.8
Зависимость объема выборки от ее ошибки36 (размер генеральной совокупности составляет 20 тыс. ед.)
| Ошибка выборки,% | |||||||||||||
| Объем выборки, ед. |
Второй тип ошибок выборки — систематические ошибки. Если социолог решил узнать мнение всех жителей города о проводимой местными органами власти социальной политике, а опросил только тех, у кого есть телефон, то возникает предумышленное смещение выборки в пользу зажиточных слоев, т.е. систематическая ошибка.
Таким образом, систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования36. Систематические ошибки считаются страшнее случайных еще и потому, что они не поддаются контролю и измерению.
Они возникают, когда, например: 1) выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд); 2) налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%); 3) отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).
Внимание! В отличие от случайных ошибок систематические ошибки при возрастании объема выборки не уменьшаются.
Обобщив все случаи, когда происходят систематические ошибки, методисты составили их реестр. Они полагают, что источником неконтролируемых перекосов в распределении выборочных наблюдений могут быть следующие факторы:
♦ нарушены методические и методологические правила проведения социологического исследования;
♦ выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
♦ произошла замена требуемых единиц наблюдения другими, более доступными;
♦ отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).
Намеренные ошибки социолог допускает редко. Чаще ошибки возникают из-за того, что социологу плохо известна структура генеральной совокупности: распределение людей по возрасту, профессии, доходам и т.д.
Систематические ошибки легче предупредить (по сравнению со случайными), но их очень трудно устранить. Предупреждать систематические ошибки, точно предвидя их источники, лучше всего заранее — в самом начале исследования.
Вот некоторые способы избежать ошибок:
♦ каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
♦ отбор желательно производить из однородных совокупностей;
♦ надо знать характеристики генеральной совокупности;
♦ при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.
Если выборочная совокупность (или просто выборка) состав-лена правильно, то социолог получает надежные результаты, ха-растеризующие всю генеральную совокупность. Если она состав-лена неправильно, то ошибка, возникшая на этапе составления выборки, на каждом следующем этапе проведения социологичес-кого исследования приумножается и достигает в конечном счете такой величины, которая перевешивает ценность проведенного исследования. Говорят, что от такого исследования больше вре-да, нежели пользы.
Подобные ошибки могут произойти только с выборочной со-вокупностыо. Чтобы избежать или уменьшить вероятность ошиб-ки, самый простой способ — увеличивать размеры выборки
(в идеале до объема генеральной: когда обе совокупности совпадут, ошибка выборки вообще исчезнет). Экономически такой метод невозможен. Остается другой путь — совершенствовать математические методы составления выборки. Они-то и применяются на практике. Таков первый канал проникновения в социологию математики. Второй канал — математическая обработка данных.
Особенно важной проблема ошибок становится в маркетинговых исследованиях, где используются не очень большие выборки. Обычно они составляют несколько сотен, реже — тысячу респондентов. Здесь исходным пунктом расчета выборки выступает вопрос об определении размеров выборочной совокупности. Численность выборочной совокупности зависит от двух факторов: 1) стоимости сбора информации и 2) стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь. Конечно, даже не искушенные в статистике и социологии люди интуитивно понимают, что чем больше размеры выборки, т.е. чем ближе они к размерам генеральной совокупности в целом, тем более надежны и достоверны полученные данные. Однако выше мы уже говорили о практической невозможности сплошных опросов в тех случаях, когда они проводятся на объектах, численность которых превышает десятки, сотни тысяч и даже миллионы. Понятно, что стоимость сбора информации (включающая оплату тиражирования инструментария, труда анкетеров, полевых менеджеров и операторов по компьютерному вводу) зависит от той суммы, которую готов выделить заказчик, и слабо зависит от исследователей. Что же касается второго фактора, то мы остановимся на нем чуть подробнее.
Итак, чем больше величина выборки, тем меньше возможная ошибка. Хотя необходимо отметить, что при желании увеличить точность вдвое вам придется увеличить выборку не в два, а в четыре раза. Например, чтобы сделать в два раза более точной оценку данных, полученных путем опроса 400 человек, вам потребуется опросить не 800, а 1600 человек. Впрочем, вряд ли маркетинговое исследование испытывает нужду в стопроцентной точности. Если пивовару необходимо узнать, какая часть потребителей пива предпочитает именно его марку, а не сорт его конкурента, — 60% или 40%, то на его планы никак не повлияет разница между 57%, 60 или 63%.
Ошибка выборки может зависеть не только от ее величины, но и от степени различий между отдельными единицами внутри генеральной совокупности, которую мы исследуем. Например, если нам нужно узнать, какое количество пива потребляется, то мы обнаружим, что внутри нашей генеральной совокупности нормы потребления у различных людей существенно различаются (гете-134
рогенная генеральная совокупность). В другом случае мы будем изучать потребление хлеба и установим, что у разных людей оно различается гораздо менее существенно {гомогенная генеральная совокупность). Чем больше различия (или гетерогенность) внутри генеральной совокупности, тем больше величина возможной ошибки выборки. Указанная закономерность лишь подтверждает то, что нам подсказывает простой здравый смысл. Таким образом, как справедливо утверждает В. Ядов, «численность (объем) выборки зависит от уровня однородности или разнородности изучаемых объектов. Чем более они однородны, тем меньшая численность может обеспечить статистически достоверные выводы»37.
Определение объема выборки зависит также от уровня доверительного интервала допустимой статистической ошибки. Здесь имеются в виду так называемые случайные ошибки, которые связаны с природой любых статистических погрешностей. В.И. Па-ниотто приводит следующие расчеты репрезентативной выборки с допущением 5%-ной ошибки38 (табл. 2.9):
Таблица 2.9
Дата добавления: 2016-11-22; просмотров: 1421;
