Р түрлі пайыздық ставканың баламалылығы
Түрлі қаржы операциялары бойынша жасалатын есептерде эквивалентті пайыздық ставканы анықтау қажет болады.
Эквивалентті пайыздық ставка – бұл әр түрлі бастапқы жағдайларда қолданылғанда бірдей қаржы нәтижесін беретін сан алуан түрдегі пайыздық ставка.
Эквивалентті пайыздық ставканы қаржы операциясының шарттарын таңдау мүмкіндігі болғанда және әр түрлі пайыздық ставканы дәлдеп салыстыру құралы қажет болған жағдайда білу керек.
Эквиваленттік пайыздық ставканы табу үшін эквиваленттік теңдеуі пайдаланылады, оны жасау принципі төмендегідей. әр түрлі пайыздық ставканы пайдалану кезінде есептеуге болатын мөлшер (әдетте бұл өсірілген S сомасы) таңдалады. Екі формула тең негізінде осы мөлшер үшін эквиваленттік теңдеуі құралады, одан тиісті қайта құру арқылы сан алуан түрдегі пайыздық ставканың арасындағы тәуелділікті көрсететін арақатынас алынады.
Қаржы операцияларының шарттары сәйкес келетін, яғни бастапқы капитал, уақытша база, пайызды есептеу әдісі (дәл немесе дағдылы) және есептеу кезеңдері бірдей жағдайды қарастырайық.. Кері жағдайда сол пікір мен түрлендіру қолданылады, тек алынған формулаларда ауыспалының саны көбірек болады. Пайыз есептеудің әр түрлі тәсілдерінде өскен соманы анықтауға арналған формулаларды қайталаймыз:
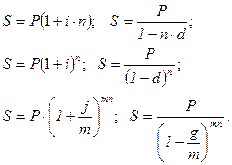
Осы формулаларды екі-екіден теңестіре отырып, кез келген екі әр түрлі пайыздық ставканың арасындағы тәуелділікті білдіретін арақатынасты алуға болады.
Бірнеше мысалды қарастырамыз.
1) 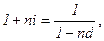 мұнда
мұнда 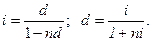
2) 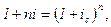 мұнда
мұнда 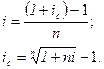
3) 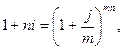 мұнда
мұнда 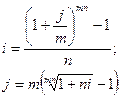
Күрделі пайыздың әр түрлі жағдайлары үшін эквиваленттің келесі теңдеуін аламыз:
4) 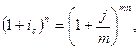 мұнда
мұнда 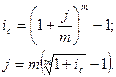
Соңғы формула бойынша алынған атаулы пайыздық ставкаға эквиваленті күрделі пайыздың жылдық ставкасы күрделі пайыздың тиімді (нақты) ставкасы деп аталады.
Қаржы операциясының іс жүзіндегі кірістілігін бағалау немесе әр түрлі есептеу аралықтары пайдаланылған жағдайда пайыздық ставканы салыстыру үшін күрделі пайыздың тиімді ставкасын білу пайдалы.
Тиімді пайыздық ставканың мағынасы атаулының мағынасынан көп, ал m = 1 болса олар үйлеседі.
5) 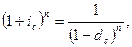 мұнда
мұнда 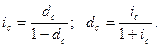
Көрнекілік материалдары:
1. Жай несие ставкасы бойынша компаудингтеу
2. Жай несие ставкасы бойынша дисконттау
3. Егер несиенің ұзақтығы бір жылдан кем болса, онда төмендегі формулаларды пайдалануға болады-
4. Пайыз есептеудің әр түрлі тәсілдерінде өскен соманы анықтауға арналған формулаларды қайталаймыз
Бақылау сұрақтары:
1. Қаржы математикасының базалық ұғымдары
2. Пайыз есептеу тәсілдері
3. Несие пайызының жай және күрделі ставкасы
4. Әртүрлі пайыздық ставканың баламалылығы
5. Қаржы шешімін қабылдағанда ақшаның инфляциялық құнсыздануын есептеу
6. Дисконттау дегеніміз не?
7. Компаудингтеу дегеніміз не?
8. Дисконтты есептеуге қажетті көрсеткіштерді атаңыз?
9. Эквивалентті пайыздық ставка дегеніміз не?
10. Эквивалентті теңдеуді қалай пайдаланамыз?
11. Егер несиенің ұзақтығы бір жылдан кем болса, онда қандай формулаларды пайдалануға болады?
12. Формулаларды түрлендіре отырып түрлі жағдайларда белгісіз мөлшерді табу үшін тағы да қандай бірнеше формулаларды аламыз?
13. Қазіргі уақытта күрделі несие пайызы түрлі қаржы операцияларында пайыздық ставканың біршама таралған түрін калай есептейміз?
14. Егер несиенің n жылдағы мерзімі бүтін сан болмаса, өсу көбейтіндісі қандай формула бойынша анықталады?
15. Дисконтты есептейтін формулаларды атап көрсетіңіз?
Дата добавления: 2016-05-11; просмотров: 3740;
