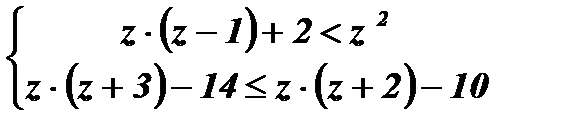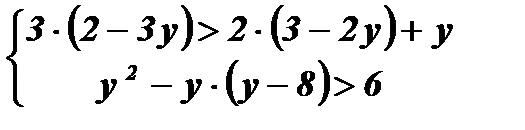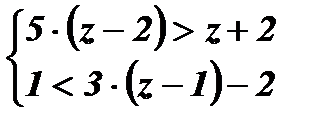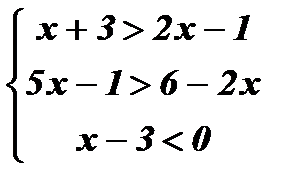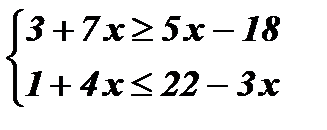Линейные неравенства и их системы
Определение: Неравенства вида 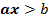 и
и 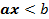 , где x - переменная, a, b - некоторые числа, называются линейными неравенствами с одной переменной.
, где x - переменная, a, b - некоторые числа, называются линейными неравенствами с одной переменной.
Определение: Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Определение: Решить неравенство - значит найти все его решения или доказать, что решений нет.
Определение: Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, называются равносильными.
Свойства:
1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
2. Если обе части неравенства умножить или разделить на одно и тоже положительное число, то получится равносильное ему неравенство.
3. Если обе части неравенства умножить или разделить на одно и тоже отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Определение: Решением системы неравенств с одной переменной, называется значение переменной, при котором верно каждое из неравенств системы.
Пример: Решить неравенства:
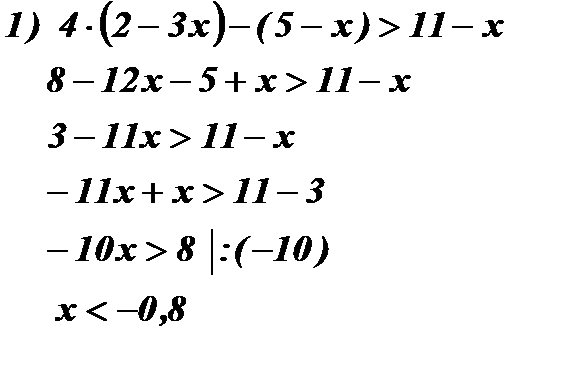
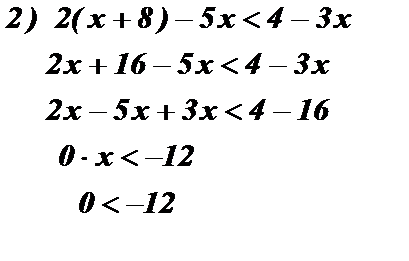
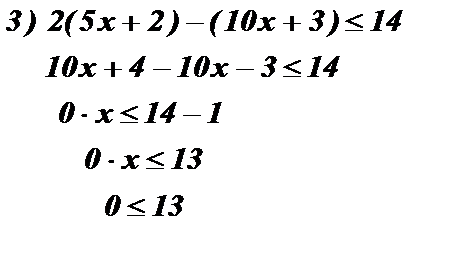
Ответ: 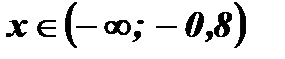 Ответ: решений нет. Ответ:
Ответ: решений нет. Ответ: 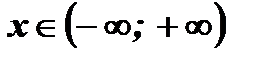
Пример: Решить систему неравенств:
| 3,5 |
| х |
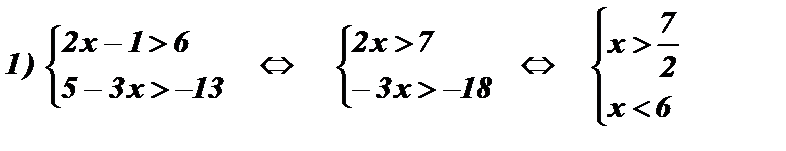
Ответ: 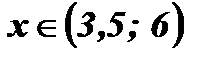
| х |
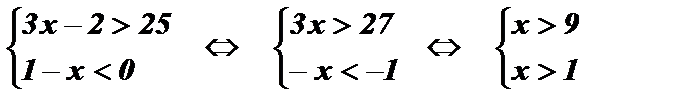
Ответ: 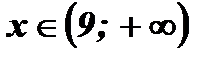
| х |
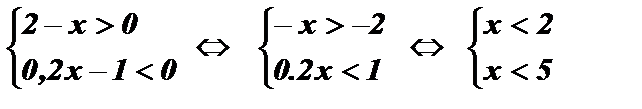
Ответ: 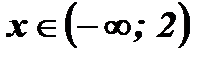
| -2 |
| х |
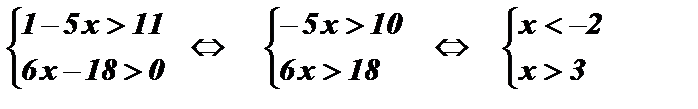
Ответ:решений нет.
5) 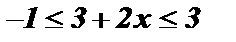
| -2 |
| х |
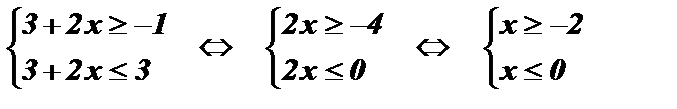
Ответ: 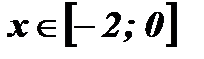
Упражнения: Решить системы неравенств:
| | |
| | |
| |
Дата добавления: 2016-11-02; просмотров: 1013;