Спектри сигналів з кутовою модуляцією

При кутовій модуляції 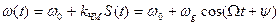(4.5)

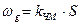- девіація частоти, відхилення частоти від нормованого значення.

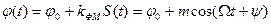(4.6)

Тут введено позначення 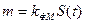- індекс фазової модуляції.

Загальний вигляд несучих коливань:

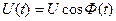(4.7)

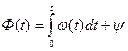(4.8)

Враховуючи (4.5) і (4.8) при ψ=0 можемо записати:

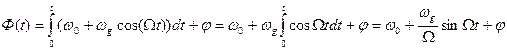
Якщо позначити 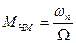, то:

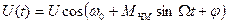(4.9)

Аналогічно, враховуючи (4.6) і (4.7) для фазо-модульованого коливання:

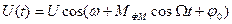(4.10)

Як видно із (4.9) та (4.10) розрізнити ФМ та ЧМ-модуляцію дуже складно. Використовуючи відоме з теорії функцій Бесселя співвідношення для комплексних функцій, можна записати:

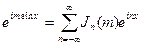, (4.11)

де J_n(m) – функція Бесселя І роду, n-ного порядку, яка визначається:

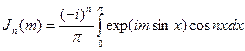(4.11а)

Враховуючи, що (4.9) та (4.10) можна описати дійсною частиною комплексного числа, тобто представити у вигляді:

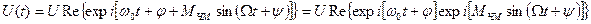(4.12)

Можна знайти спектр ЧМ та ФМ-коливань, якщо перейти в (4.12) до тригонометричної форми запису, тоді другу експоненту можна записати у вигляді суми ряду (4.11).

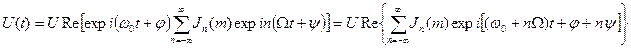(4.13)

Враховуючи те, що дійсна частина є сумою дійсних частин доданків суми ряду, а також співвідношення для коефіцієнтів функції Бесселя (4.11а) в кінцевому вигляді (4.13) буде мати вигляд:

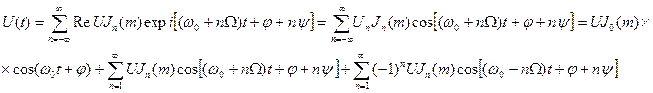(4.14)

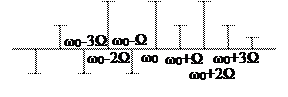Одержаний спектр складається з безмежного числа бічних гармонік ω₀±nΩ, однак для непарних верхніх і нижніх складових фазові коливання знаходяться в протифазі.