Незалежність у сукупності та попарна незалежність випадкових подій

Означення 6.3. Випадкові події А₁, А₂, ... , А_n називаються незалежними у сукупності, якщо для будь-якого 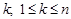, і для будь-якого набору індексів 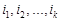таких, що 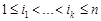виконується рівність

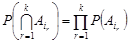. (6.7)

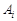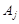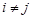Зокрема, якщо випадкові події А₁, А₂, ... , А_n – незалежні у сукупності, то будь-які дві події і , будуть незалежними, тобто має місце попарна незалежність двох подій. Проте з попарної незалежності ще не випливає, взагалі кажучи, незалежність у сукупності. Пояснимо це на прикладі.

Приклад Бернштейна. На площину кидають тетраедр, три грані якого пофарбовані відповідно в червоний, зелений, блакитний кольори, а на четверту грань нанесені всі три кольори. Нехай випадкові події А, В, С означають, що при киданні тетраедра випала грань, на якій присутній відповідний колір. Оскільки кожний колір нанесено на дві грані тетраедра, то

.

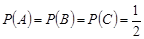Два кольори має тільки одна грань, тому

.

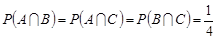Отже, випадкові події А, В, С – попарно незалежні, бо

, , .

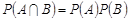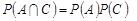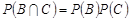Всі три кольори нанесені тільки на одну грань, тому

.

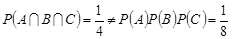Це означає, що події А, В, С – не є незалежними у сукупності.

Розглянемо деякі приклади на застосування введених понять незалежних у сукупності та попарно незалежних випадкових подій.