Мода та медіана випадкової величини
Означення 11.6. Модою дискретної випадкової величини  називається її найбільш імовірне значення, тобто таке значення
називається її найбільш імовірне значення, тобто таке значення  , ймовірність якого
, ймовірність якого 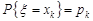 – найбільша.
– найбільша.
Означення 11.7. Модою неперервної випадкової величини  називається абсциса точки максимуму щільності розподілу
називається абсциса точки максимуму щільності розподілу  .
.
Означення 11.8. Розподіл випадкової величини називається унімодальним, якщо він має одну моду, та полімодальним, якщо він має декілька мод.
Якщо щільність розподілу ймовірностей  не має максимуму, а має мінімум, то такий розподіл іноді називають антимодальним. Прикладом антимодального розподілу є “закон арксинусу” з щільністю розподілу
не має максимуму, а має мінімум, то такий розподіл іноді називають антимодальним. Прикладом антимодального розподілу є “закон арксинусу” з щільністю розподілу
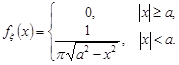
Означення 11.9. Медіаною випадкової величини  (як правило неперервної) називається таке значення
(як правило неперервної) називається таке значення 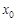 , для якого
, для якого
 .
.
Отже, медіана характеризує таке значення випадкової величини, що ймовірність набути значення менше за медіану та ймовірність набути значення більші за медіану, дорівнюють між собою. Інакше кажучи, медіана – це абсциса точки, яка поділяє площу під кривою розподілу на рівні частини.
Приклад 11.5. Знайти моду та медіану неперервної випадкової величини  , щільність розподілу якої має вигляд
, щільність розподілу якої має вигляд
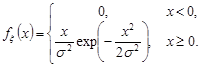
Цей розподіл є розподіл Релея.
Розв’язання. Для визначення моди випадкової величини  знайдемо максимум функції
знайдемо максимум функції  при
при 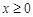 .
.
 = 0, якщо
= 0, якщо  .
.
Легко перевірити, що саме в точці  буде максимум. Отже, мода розподілу Релея дорівнює
буде максимум. Отже, мода розподілу Релея дорівнює  .
.
Медіану випадкової величини  знайдемо з умови
знайдемо з умови 
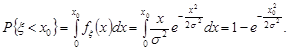
Із рівняння  маємо
маємо 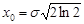 .
.
Дата добавления: 2016-11-02; просмотров: 2785;
