Математичне сподівання випадкової величини
Закон розподілу випадкової величини, як би він не був записаний, повністю задає випадкову величину. Однак в деяких прикладних задачах достатньо мати лише деяке сумарне уявлення про найбільш характерні риси розподілу випадкової величини. Для прикладних застосувань теорії ймовірностей важливу роль мають деякі детерміновані (невипадкові) величини, які характеризують деяким чином поведінку випадкових величин. До цих сталих величин належать, перш за все, математичне сподівання, дисперсія, моменти. Введемо означення.
Означення 11.1. Якщо  – дискретна випадкова величина, яка має розподіл
– дискретна випадкова величина, яка має розподіл
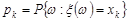 , k = 1, 2,... ,
, k = 1, 2,... ,
то її математичним сподіванням називається ряд, який визначається за формулою
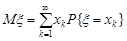 . (11.1)
. (11.1)
Ряд (11.1) має збігатися абсолютно, в супротивному випадку кажуть, що випадкова величина не має математичного сподівання. Абсолютна збіжність ряду потрібна для того, щоб сума ряду (11.1) не залежала від порядку нумерації значень випадкової величини. Якщо величина  набуває лише скінчену множину значень, то ряд (11.1) буде скінченою сумою.
набуває лише скінчену множину значень, то ряд (11.1) буде скінченою сумою.
Означення 11.2. Якщо  – неперервна випадкова величини, яка має щільність розподілу ймовірностей
– неперервна випадкова величини, яка має щільність розподілу ймовірностей  , то її математичним сподіванням називається величина, яка визначається інтегралом
, то її математичним сподіванням називається величина, яка визначається інтегралом
 (11.2)
(11.2)
за умови, що цей інтеграл збігається абсолютно.
Математичне сподівання, як числова характеристика випадкової величини, характеризує її середнє значення. Це видно з механічної інтерпретації математичного сподівання. Якщо припустити, що матеріальна точка з абсцисою 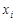 має масу, що дорівнює
має масу, що дорівнює 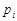 (
(  2, ..., n), а вся одинична маса
2, ..., n), а вся одинична маса 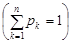 розподілена між цими точками, то математичне сподівання задає абсцису центра мас системи матеріальних точок. Якщо ж одинична маса розподілена неперервно на прямій з щільністю
розподілена між цими точками, то математичне сподівання задає абсцису центра мас системи матеріальних точок. Якщо ж одинична маса розподілена неперервно на прямій з щільністю  , то математичне сподівання можна інтерпретувати як центр тяжіння цієї маси. Наведемо приклади обчислення математичного сподівання випадкових величин.
, то математичне сподівання можна інтерпретувати як центр тяжіння цієї маси. Наведемо приклади обчислення математичного сподівання випадкових величин.
Приклад 11.1. За умовою задачі прикладу 9.2 обчислити математичне сподівання випадкової величини  , яка задає кількість влучень при трьох пострілах
, яка задає кількість влучень при трьох пострілах
Розв’язання. Беручи до уваги ряд розподілу випадкової величини  (приклад 9.2) та формулу 11.1, маємо
(приклад 9.2) та формулу 11.1, маємо
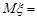 0·0,343+1·0,441+2·0,189+3·0,027=0,9.
0·0,343+1·0,441+2·0,189+3·0,027=0,9.
Приклад 11.2. В умовах прикладу 10.1 обчислити математичне сподівання неперервної випадкової величини  , яка розподілена за законом Сімпсона.
, яка розподілена за законом Сімпсона.
Розв’язання. У прикладі 10.1 було отримано щільність розподілу випадкової величини 
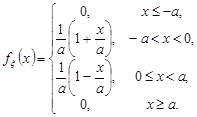
Отже, за формулою (11.2) маємо
 ,
,
оскільки інтегрується непарна функція по симетричному проміжку.
Наведемо основні властивості математичного сподівання.
1. Математичне сподівання сталої величини дорівнює нулю, тобто MC= C, де C – будь-яка стала.
Доведення. Сталу величину можна розглядати як випадкову величину, що набуває тільки одного значення С з імовірністю 1. Отже, за формулою (11.1)
MC =  =C.
=C.
2. Постійний множник виноситься за знак математичного сподівання, тобто 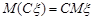 .
.
Ця властивість випливає з відповідної властивості рядів і інтегралів.
3. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань доданків, за умовою, що останні існують, зокрема для двох доданків 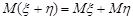 .
.
Доведення наведемо для дискретних випадкових величин.
Нехай 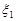 та
та 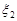 – дискретні випадкові величини і
– дискретні випадкові величини і 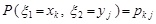 , тоді випадкова величина
, тоді випадкова величина  матиме ряд розподілу
матиме ряд розподілу
 ,
, 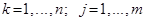 .
.
Тоді

= 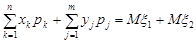 .
.
Доведення для неперервних випадкових величин простіше провести після вивчення теми “Функції від випадкових аргументів”.
4. Для формулювання наступної властивості математичного сподівання введемо поняття незалежних випадкових величин.
Означення 11.3. Нехай 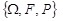 – імовірнісний простір, на якому задані випадкові величини
– імовірнісний простір, на якому задані випадкові величини  та
та 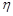 . Назвемо ці величини незалежними, якщо незалежні події
. Назвемо ці величини незалежними, якщо незалежні події  та
та 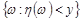 при будь-яких дійсних значеннях
при будь-яких дійсних значеннях  та
та 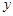 .
.
Незалежність випадкових величин означає, що
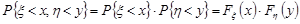 .
.
Якщо 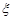 та
та 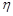 незалежні випадкові величини, то
незалежні випадкові величини, то
 .
.
Доведення наведемо для дискретних випадкових величин.
Нехай  та
та 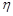 – незалежні дискретні випадкові величини, закони розподілу яких задані:
– незалежні дискретні випадкові величини, закони розподілу яких задані:
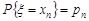 , n = 1, 2, … ;
, n = 1, 2, … ; 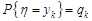 , k = 1, 2, … .
, k = 1, 2, … .
Із незалежності випадкових величин випливає рівність
 .
.
Із означення математичного сподівання 11.1 маємо
 .
.
Дата добавления: 2016-11-02; просмотров: 2404;
