Моменти випадкової величини
Поняття моменту в механіці використовують для характеристики розподілу мас. Аналогічно в теорії ймовірностей вводиться поняття моментів випадкової величини для опису властивостей розподілу ймовірностей. Дамо означення початкових та центральних моментів випадкової величини.
Означення 11.4. Початковим моментом порядку s випадкової величини  називається математичне сподівання s – го степеня цієї величини:
називається математичне сподівання s – го степеня цієї величини:
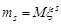 .
.
Очевидно, що  , тобто перший початковий момент співпадає с математичним сподіванням.
, тобто перший початковий момент співпадає с математичним сподіванням.
Якщо  – дискретна випадкова величини, яка має розподіл
– дискретна випадкова величини, яка має розподіл 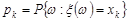 , k = 1, 2,... , то її початкові моменти обчислюють за формулою
, k = 1, 2,... , то її початкові моменти обчислюють за формулою
 .
.
Якщо  – неперервна випадкова величини, яка має щільність розподілу ймовірностей
– неперервна випадкова величини, яка має щільність розподілу ймовірностей  , то її початкові моменти знаходять так:
, то її початкові моменти знаходять так:

Доведення цих формул краще провести після вивчення теми “Функції від випадкових аргументів”.
Означення 11.5. Центральним моментом порядку s випадкової величини  називається величина
називається величина
 .
.
Очевидно, що  ,
, 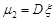 .
.
Якщо  – дискретна випадкова величини, яка має розподіл
– дискретна випадкова величини, яка має розподіл 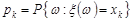 , k = 1, 2,... , то її центральні моменти обчислюють за формулою
, k = 1, 2,... , то її центральні моменти обчислюють за формулою
 .
.
Якщо  – неперервна випадкова величина, яка має щільність розподілу ймовірностей
– неперервна випадкова величина, яка має щільність розподілу ймовірностей  , то її центральні моменти знаходять так:
, то її центральні моменти знаходять так:

Між початковими та центральними моментами неважко встановити зв’язок. А саме

 .
.
Наприклад,
 ,
, 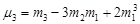 ,
,
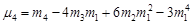 .
.
Надалі деякі моменти будемо використовувати при вивченні розподілу випадкових величин та в математичній статистиці.
Дата добавления: 2016-11-02; просмотров: 1907;
