Вторая форма условий равновесия.
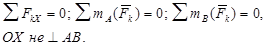

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно двух точек А и В и сумма их проекций на ось ОX, не перпендикулярную прямой АВ, были равны нулю.
2.4.4 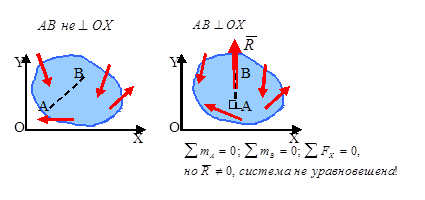 Третья форма условий равновесия.
Третья форма условий равновесия.
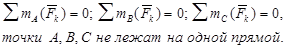
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трех точек А, В и С, не лежащих на одной прямой, были равны нулю.
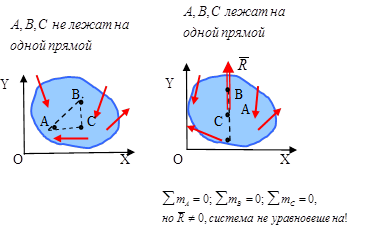 Для проверки решения задачи на равновесие плоской системы сил составляют сумму моментов всех сил относительно других точек или строят в масштабе многоугольник всех сил, действующих на тело. Если проверочное уравнение обращается в тождество, а многоугольник сил замкнут, то задача решена верно.
Для проверки решения задачи на равновесие плоской системы сил составляют сумму моментов всех сил относительно других точек или строят в масштабе многоугольник всех сил, действующих на тело. Если проверочное уравнение обращается в тождество, а многоугольник сил замкнут, то задача решена верно.
Вопросы для самоконтроля
Ø Что называется парой сил? Что происходит с телом под действием пары сил?
Ø Чему равен и как направлен вектор-момент пары сил?
Ø Когда момент пары сил считают алгебраической величиной? Как определяют модуль и знак момента пары сил в этом случае?
Ø При каком условии две пары будут эквивалентны?
Ø Как складывают пары сил, лежащие в одной плоскости? В разных плоскостях?
Ø В чем состоит условие равновесия системы пар?
Ø Что называют моментом силы относительно данной точки (центра)? Как выбирают направление вектора-момента?
Ø Когда момент силы относительно точки считают алгебраической величиной? Как определяют его модуль и знак?
Ø В каком случае момент силы относительно точки равен нулю?
Ø Изменится ли момент силы относительно данной точки при переносе силы по линии ее действия?
Ø Чему равен момент пары сил относительно данной точки (центра)?
Ø Что называется главным вектором данной системы сил?
Ø Что называется главным моментом системы сил относительно данной точки (центра)?
Ø Изменяются ли главный вектор и главный момент данной системы сил при перемене центра приведения?
Ø При каком условии главный момент плоской системы сил не зависит от выбора центра приведения?
Ø Как формулируются векторное и аналитическое условия равновесия плоской произвольной системы сил?
Ø В чем состоит теорема Вариньона? Как с ее помощью упрощают решение задач?
ЛЕКЦИЯ №3
Параллельные силы
 Система сил
Система сил 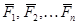 , линии действия которых параллельны друг другу и лежат в одной плоскости, называется плоской системой параллельных сил.
, линии действия которых параллельны друг другу и лежат в одной плоскости, называется плоской системой параллельных сил.
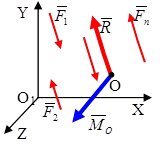
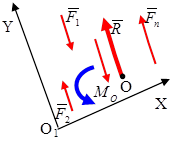
Пусть все силы лежат в плоскости О1XY.
При приведении этой системы сил к произвольному центру (точке) О получим главный вектор 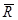 , приложенный в точке О, и пару сил с моментом
, приложенный в точке О, и пару сил с моментом 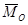 .
.
Главный вектор 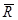 системы параллельных сил параллелен силам:
системы параллельных сил параллелен силам:
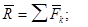
Момент пары сил 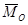 равен главному моменту параллельных сил
равен главному моменту параллельных сил 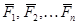 относительно центра приведения О и параллелен оси O1Z.
относительно центра приведения О и параллелен оси O1Z.
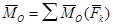 .
.
Условия равновесия для плоской системы параллельных сил в векторной форме имеют вид:
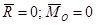 .
.
Расположим ось О1Y параллельно силам 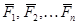 , тогда вектор
, тогда вектор 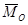 перпендикулярен плоскости О1XY и его можно считать величиной алгебраической
перпендикулярен плоскости О1XY и его можно считать величиной алгебраической 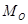
Отсюда следуют двеформы аналитических условий равновесия для системы параллельных сил на плоскости.
Дата добавления: 2016-05-11; просмотров: 1854;
