Теория пар сил, свойства пар сил
Основные понятия.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил ( 
). Плоскость, в которой лежат силы 
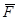и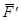 
, называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил - плечом пары.
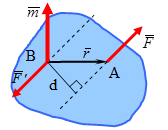Пара сил не может быть заменена одной эквивалентной ей силой, т.е. не имеет равнодействующей, так как 
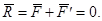Пара может быть уравновешена только другой парой сил.
Под действием пары сил тело вращается. Вращательный эффект пары, характеризуется моментом пары.
Моментом пары называется вектор равный векторному произведению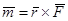 
, модуль которого равен произведению модуля одной из сил пары на ее плечо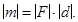 
Вектор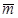 
направлен перпендикулярно плоскости пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Момент пары 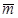- свободный вектор, т. е. его можно прикладывать в любой точке тела.
Свойства пар сил.
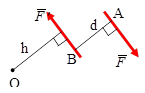1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О: 
.
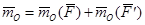2. Момент пары относительно любого центра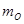 
равен моменту пары m: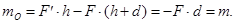 
3. Момент пары равен моменту одной из сил пары относительно точки приложения другой силы пары: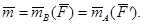 
Теорема 1. Пары сил с равными моментами эквивалентны.
Следствия:
1. Пару сил, приложенную к твердому телу,можно заменить другой парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:
2.Пару сил можно переносить в плоскость, параллельную плоскости пары.
Теорема 2. Совокупность нескольких пар с моментами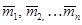 
эквивалентна одной паре, момент 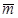которой равен геометрической сумме моментов данных пар:
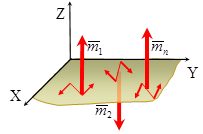
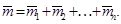
Если пары лежат в одной плоскости, то момент пары считают величиной алгебраической, так как в этом случае все вектора моментов пар параллельны. Алгебраический момент пары равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары:
.
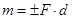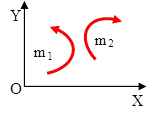Знак «+» соответствует повороту тела под действием пары против хода часовой стрелки, «─» - по ходу часовой стрелки.
Пары сил на плоскости часто изображается дуговой стрелкой, показывающей направление поворота тела парой.
Согласно теореме 2 на плоскости пары можно заменить одной парой с моментом равным алгебраической сумме моментов пар:
m = m1 + m2 + ... + mn.
Если на тело действуетплоская система пар, то тело находится в равновесии, если сумма моментов пар равна нулю:
.
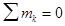Дата добавления: 2016-05-11; просмотров: 1360;