Непосредственное интегрирование
Метод непосредственного интегрирования является одним из простейших методов интегрирования.
Он опирается на:
1) таблицу интегралов;
2) основные свойства неопределенных интегралов.
Рассмотрим несколько примеров на применение метода непосредственного интегрирования:
Пример 6.6.8.Найти неопределенный интеграл 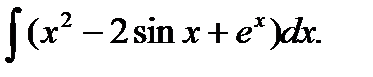
I = (использовать свойства 4 и 3; формулы 2,4а,6таблицы простейших интегралов.) = = 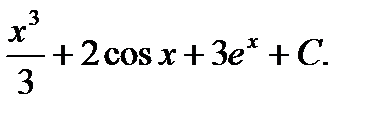

Проверка: 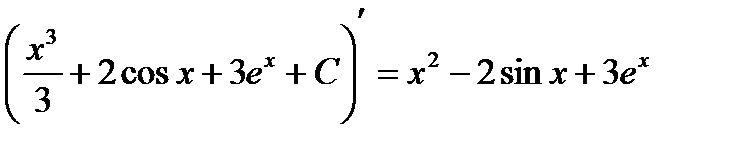
Пример 6.6.9. 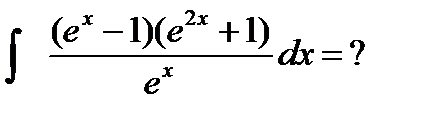
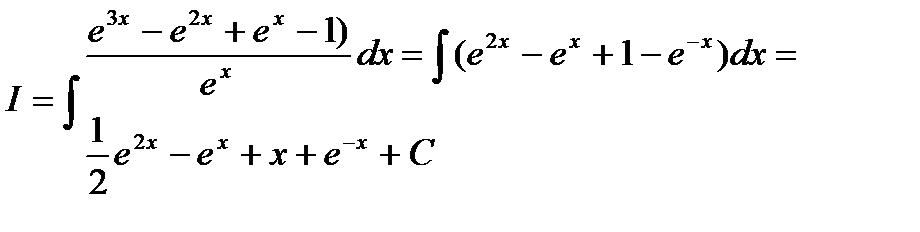 .
.
Пример 6.6.10. 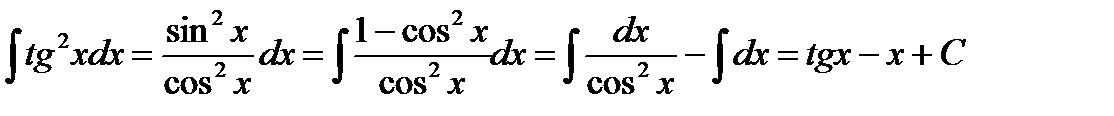 .
.
Пример 6.6.11. 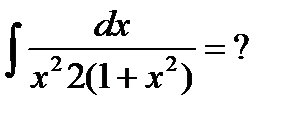
Прибавим и вычтем в числителе 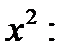
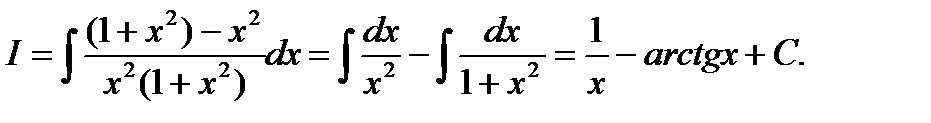
В некоторых случаях сложное на первый взгляд выражение, стоящее под знаком интеграла, удается преобразовать и свести к простейшим формулам интегрирования:
Пример 6.6.12. 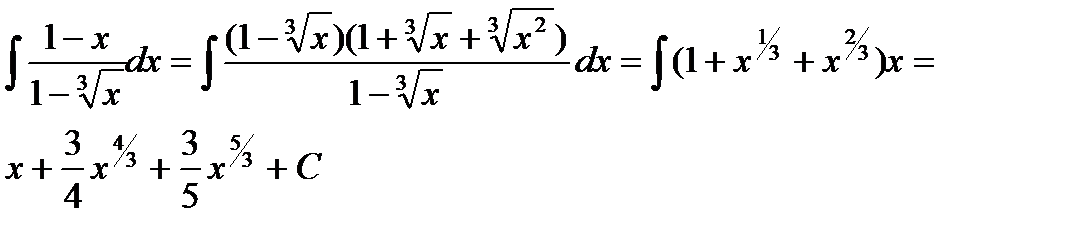 .
.
Замечание. В таблице основных интегралов предполагалось, что х является независимой переменной.
Однако формулы этой таблицы остаются справедливыми и в случае, когда 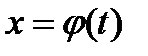 ; где
; где 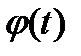 - любая дифференцируемая функция новой переменной t.
- любая дифференцируемая функция новой переменной t.
Доказано, пусть (*) 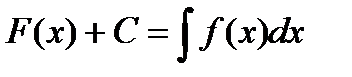 ,
, 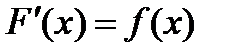 ,и пусть
,и пусть 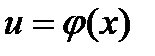 дифференцируемая функция х.
дифференцируемая функция х.
В силу инвариантности формы первого дифференциала
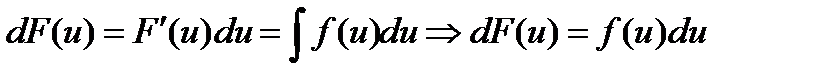 , откуда
, откуда 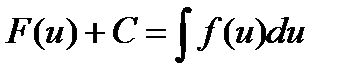 (**)
(**) 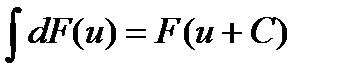
Итак, из справедливости формулы (*) следует справедливость формулы (**), которая получается из первой формулы формальной заменой х на U.
На основании этого свойства получаем обобщенную таблицу простейших интегралов.
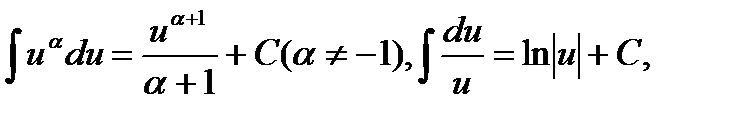
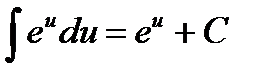 ,
, 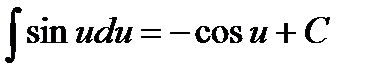
и т. д., где u – любая дифференцируемая функция х.
Примеры 6.6.12.
1) 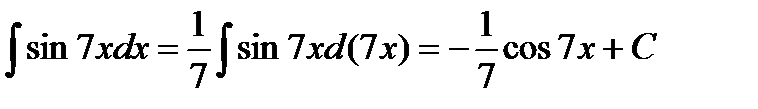 ;
;
2) 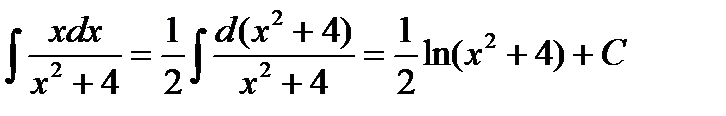 ;
;
3) 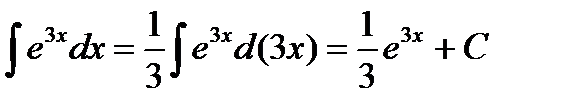 ;
;
Дата добавления: 2016-10-17; просмотров: 1215;
