Смешанное расширение игры

Рассмотрим матричную игру G. Если в ней существует ситуация равновесия, то минимакс равен максимину. Причем каждый из игроков может сообщить другому игроку информацию о своей оптимальной стратегии. Его соперник не сможет извлечь из этой информации никакой дополнительной выгоды. Теперь предположим, что в игре G нет ситуации равновесия. Тогда:

(2.17)

В этом случае минимаксная и максиминная стратегии не являются устойчивыми. Игроки могут иметь стимулы к отклонению от своих осторожных стратегий, связанные с возможностью получения большего выигрыша, но и с риском проигрыша, то есть получения выигрыша меньшего, чем при применении осторожной стратегии. При применении рискованных стратегий передача информации о них противнику имеет пагубные последствия: игрок автоматически получает выигрыш меньший, чем при применении осторожной стратегии.

Пример 3. Пусть матрица игры имеет вид:

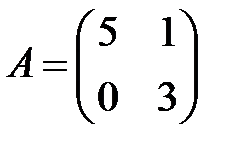
Для такой матрицы 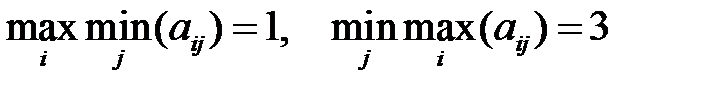, т.е. ситуации равновесия не существует. Осторожными стратегиями игроков являются i*=1, j*=2. Пусть игрок 2 придерживается стратегии j*=2, а игрок 1 выберет стратегию i=2. тогда последний получит выигрыш 3, что на две единицы больше, чем максимин. Если, однако, игрок 2 догадается о планах игрока 1, он сменит свою стратегию на j=1, и тогда первый получит выигрыш 0, то есть меньше своего максимина. Аналогичные рассуждения можно провести и для второго игрока. В целом можно сделать вывод, что применение авантюрной стратегии может в отдельной партии игры принести результат больший, чем гарантированный, но ее применение связано с риском. Возникает вопрос, нельзя ли скомбинировать надежную осторожную стратегию с авантюрной таким образом, чтобы увеличить свой средний выигрыш? По существу вопрос стоит о том, как разделить между игроками выигрыш (2.17)?

Оказывается, что разумным решением является применение смешанной стратегии, то есть случайный выбор чистых стратегий. Напомним, что стратегия игрока 1 называется смешанной, если выбор i-ой строки производится им с некоторой вероятностью p_i. Такую стратегию можно отождествить с распределением вероятностей 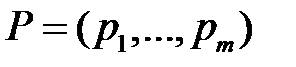на множестве строк. Предположим, что первый игрок имеет m чистых стратегий, а второй – n чистых стратегий. Тогда их смешанные стратегии – это вероятностные вектора:

(2.18)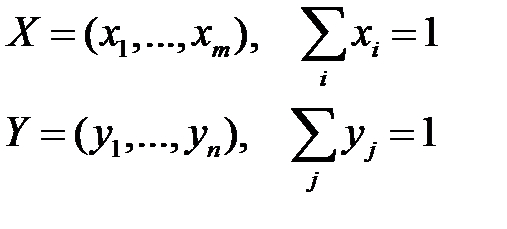

Рассмотрим две возможные смешанные стратегии первого игрока из примера 3: . Эти стратегии отличаются распределениями вероятностей между чистыми стратегиями. Если в первом случае строки матрицы выбираются игроком с равными вероятностями, то во втором случае – с разными. Когда мы говорим о смешанной стратегии, то имеем ввиду под случайным выбором не выбор «наобум», а выбор, основанный на работе случайного механизма, обеспечивающего нужное нам распределение вероятностей. Так для реализации первой из смешанных стратегий хорошо подходит подбрасывание монетки. Игрок выбирает первую строку или вторую в зависимости от того, как выпадет монетка. В среднем игрок будет одинаково часто выбирать как первую строку, так и вторую, однако выбор на конкретной итерации игры не подчинен никакому фиксированному правилу и обладает максимальной степенью скрытности: до реализации случайного механизма он неизвестен даже самому первому игроку. Для реализации второй смешанной стратегии хорошо подходит механизм жеребьевки. Игрок берет семь одинаковых бумажек, пометив три их них крестиком, и бросает в шапку. Затем, наудачу, извлекает одну из них. Согласно классической теории вероятностей он вытащит бумажку с крестиком с вероятностью 3/7, а чистую бумажку – с вероятностью 4/7. Подобный механизм жеребьевки способен реализовывать любые рациональные вероятности.

Пусть игроки придерживаются смешанных стратегий (2.18). Тогда выигрыш первого игрока на отдельно взятой итерации игры является случайной величиной: v(X,Y). Поскольку игроки выбирают стратегии независимо друг от друга, то, согласно теореме умножения вероятностей, вероятность выбора исхода (i,j) с выигрышем 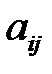равна произведению вероятностей . Тогда закон распределения случайной величины v(X,Y) задан следующей таблицей

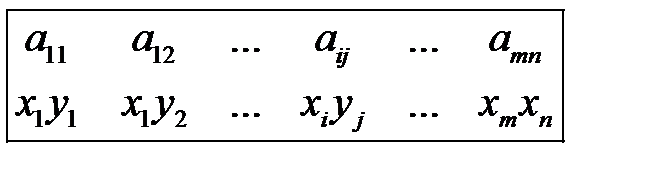
Пусть теперь игра разыгрывается бесконечно долго. Тогда средний выигрыш в такой игре равен математическому ожиданию величины v(X,Y).

(2.19)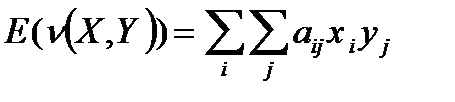

При конечном, но достаточно большом числе итераций игры средний выигрыш будет незначительно отличаться от величины (2.19).

Пример 4. Рассчитаем средний выигрыш (2.19) для игры из примера 3 при использовании игроками следующих стратегий: 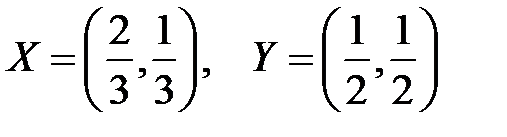. Матрица выигрышей и матрица вероятностей выглядят следующим образом:

Найдем среднее:

(2.20)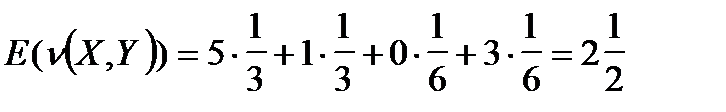

Таким образом, средний выигрыш (2.20) имеет промежуточное значение между максимином и минимаксом.

Поскольку для любой пары смешанных стратегий X и Y можно подсчитать среднее значение игры, то возникает задача о поиске оптимальной стратегии. Естественно начать с исследования осторожных стратегий. Осторожная стратегия первого игрока обеспечивает ему максимин. Осторожная стратегия второго игрока не позволяет первому выиграть более минимакса. Самым значительным результатом в теории игр с противоположными интересами можно считать следующий:

Теорема. Всякая матричная игра имеет ситуацию равновесия в смешанных стратегиях. Доказательство данной теоремы непросто. В данном курсе оно опускается.

Следствия: Существование ситуации равновесия означает, что максимин равен минимаксу, и следовательно, любая матричная игра имеет цену. Оптимальной стратегией первого игрока является максиминная стратегия. Оптимальной стратегией второго – минимаксная. Поскольку задача поиска оптимальных стратегий решена, то говорят, что любая матричная игра разрешима на множестве смешанных стратегий.

Решение игры 2х2

Пример 5. Решить игру 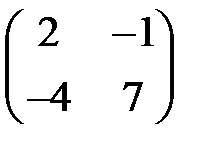. Не трудно убедиться, что седловой точки нет. Обозначим оптимальную стратегию первого игрока (х, 1-х) – это вектор столбец, но для удобства записываем его в виде строки. Оптимальную стратегию второго игрока обозначим (y,1-y).

Выигрыш первого игрока есть случайная величина со следующим распределением:

Находим средний выигрыш за итерацию первого игрока – математическое ожидание случайной величины v(x,y):

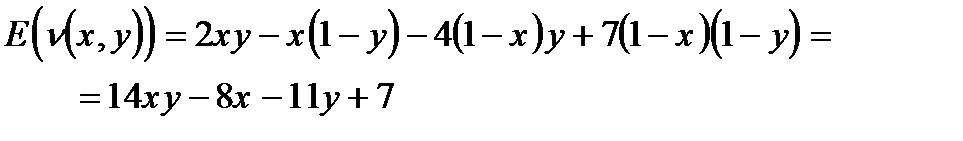
Преобразуем данное выражение:

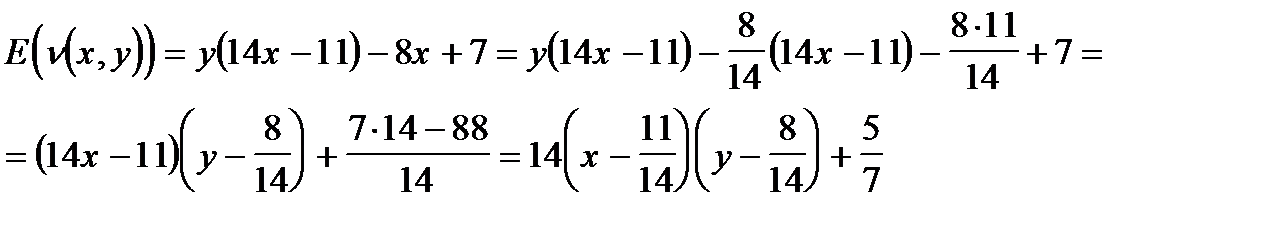
Данное математическое ожидание состоит из константы (5/7) и переменной части: 14(x-11/14)(y-8/14). Если значение y отличается от 8/14, то первый игрок всегда может выбрать х таким образом, чтобы сделать переменную часть положительной, увеличивая свой выигрыш. Если значение х отличается от 11/14, то второй игрок всегда может выбрать y таким образом, чтобы сделать переменную часть отрицательной, уменьшая выигрыш первого игрока. Таким образом, седловая точка определяется равенствами: x*=11/14, y*=8/14.

2.5 Решение игр

Способ решения подобных игр покажем на примере.

Пример 6. Решить игру 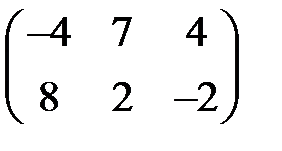. Убеждаемся, что седловой точки нет. Обозначим смешанную стратегию первого игрока X=(х, 1-х) – это вектор столбец, но для удобства записываем его в виде строки.

Пусть первый игрок применяет стратегию Х, а второй – свою j-ю чистую стратегию. Обозначим средний выигрыш первого игрока в этой ситуации как 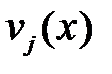. Имеем:

(2.21)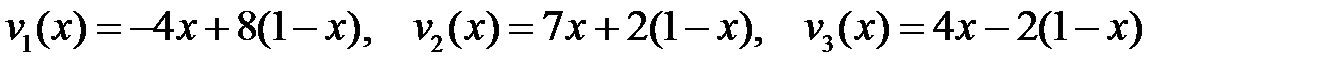

Изобразим графики функций (2.21) на отрезке [0,1].

Ордината точки, находящейся на любом из отрезков прямых, соответствует выигрышу первого игрока в ситуации, когда он применяет смешанную стратегию (х,(1-х)), а второй игрок – соответствующую чистую стратегию. Гарантированный результат первого игрока – это нижняя огибающая семейства прямых (ломанная АВС). Наивысшая точка этой ломанной (точка В) является максимальным гарантированным результатом игрока 1. Абсцисса точки В соответствует оптимальной стратегии первого игрока.

Поскольку искомая точка В является пересечением линий и 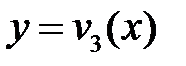, то ее абсцисса 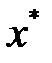может быть найдена как решение уравнения:

Таким образом, оптимальная смешанная стратегия первого игрока – (5/9, 4/9). Ордината точки В является ценой игры. Она равна:

(2.22)

Заметим, что линия, соответствующая второй стратегии второго игрока проходит выше точки В. Это означает, что если первый игрок применяет свою оптимальную стратегию, а игрок 2 – вторую, то проигрыш второго увеличивается по сравнению с применением стратегий 1 или 3. Таким образом, вторая стратегия не должна участвовать в оптимальной стратегии второго игрока. Оптимальная стратегия игрока 2 должна иметь вид: 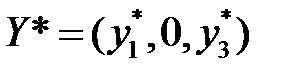. Чистые стратегии 1 и 3 второго игрока, имеющие в оптимальной стратегии ненулевые составляющие, принято называть существенными. Стратегия 2 называется несущественной. Из рисунка выше, а также из равенства (2.22) видно, что при применении первым игроком своей оптимальной стратегии выигрыш второго игрока не зависит от того, какую из своих существенных стратегий он применяет. Он может применить также любую смешанную стратегию, состоящую из существенных (в частности – оптимальную), выигрыш и в этом случае не изменится. Совершенно аналогичное утверждение справедливо и для противоположного случая. Если второй игрок применяет свою оптимальную стратегию, то выигрыш первого игрока не зависит от того, какую из своих существенных стратегий он применяет и равен цене игры. Пользуясь этим утверждением, найдем оптимальную стратегию второго игрока.

Пусть оптимальная стратегия игрока 2 есть Y*=(y*, 0, 1-y*) и пусть первый игрок использует свою первую чистую стратегию. Тогда:

Таким образом, оптимальная стратегия второго игрока : Игра полностью решена.