Инспекционные игры в контролировании вооружений
В качестве примера рассмотрим одну из инспекционных игр. В связи с заключением нескольких международных договоров о запрещении, нераспространении или сокращении некоторых видов вооружений возникает проблема проверки (верификации) выполнения сторонами этих договоров и соглашений. Чаще всего проверка осуществляется в форме периодических инспекций. Данная ситуация моделируется при помощи игры с нулевой суммой двух лиц: инспектора и инспектируемого. Предполагается, что инспектируемый имеет интерес в тайном нарушении соглашения. Задача игры – найти оптимальную схему инспекций, при которой инспектируемый удерживался бы от нарушений.
Рассмотрим одну из первых моделей этого плана, разработанную Дрешером[1]. Игра происходит в n стадий. Инспектор на каждой стадии может осуществлять или не осуществлять инспекцию. Он имеет возможность распределить ограниченное число m инспекций на n стадий игры. Инспектируемый на каждой стадии может либо действовать легально, так как это и предписано договором, либо допустить нарушение. Нарушение допускается не более одного раза за игру. Если оно допущено на стадии, когда осуществляется проверка, то нарушение обнаруживается и инспектор выигрывает единицу, а игра на этом заканчивается. Если оно допускается при отсутствии проверки, то инспектируемый выигрывает единицу. В остальных случаях выигрыши игроков равны нулю, а игра продолжается. Предполагается, что инспектируемый знает о проводящейся инспекции и знает общей число инспекций m.
Обозначим максиминый выигрыш инспектора как I(n,m), где  . Если инспектор обладает возможностью провести инспекцию на каждой стадии игры (m=n), то инспектируемый не может допустить нарушения. С другой стороны, если у инспектора не осталось проверок, то инспектируемый может свободно нарушать условия соглашения. Таким образом, имеем «начальные условия»:
. Если инспектор обладает возможностью провести инспекцию на каждой стадии игры (m=n), то инспектируемый не может допустить нарушения. С другой стороны, если у инспектора не осталось проверок, то инспектируемый может свободно нарушать условия соглашения. Таким образом, имеем «начальные условия»:
(2.23) 
Изобразим матрицу для первой стадии игры:
| Инспектор | Инспектируемый | |
| легальное действие | нарушение | |
| инспекция | I(n-1,m-1) | +1 |
| нет инспекции | I(n-1,m) | -1 |
Если инспектируемый проводит легальное действие, то игра продолжается и выигрыш инспектора – это выигрыш в игре, имеющей на одну стадию меньше и либо на одну проверку меньше, либо столько же проверок, в зависимости от того, использовалась инспектором на первой стадии проверка или нет.
Если инспектор применяет оптимальную смешанную стратегию (х,1-х) на первой стадии игры, то его выигрыш не зависит от того, какую чистую стратегию применяет инспектируемый. Поэтому:
(2.24) 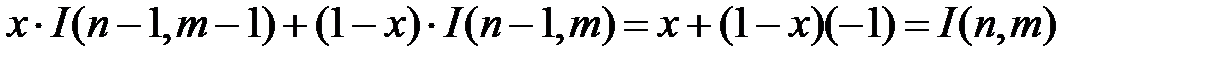
Исключая из системы (2.24) переменную х, можно получить следующее рекуррентное соотношение:
(2.25) 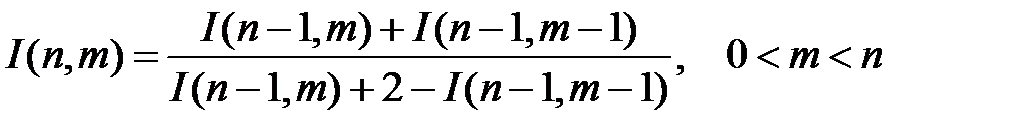
Соотношение (2.25) вместе с начальными условиями (2.23) определяет рассматриваемую нами игру для всех значений параметров. Игра может быть легко решена на современном персональном компьютере. Дрешер показал, что существует ее явное решение в виде:
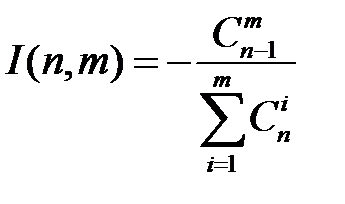
Пусть, например, n=2, m=1. Тогда, согласно (2.25) и (2.23), имеем:

Используя (2.24), получаем оптимальную стратегию инспектора для этого случая:

Дата добавления: 2016-10-17; просмотров: 638;
