Ситуация равновесия. Теоремы о седловой точке

В антагонистической игре естественно считать оптимальным такой исход, при котором ни одному из игроков невыгодно от него отклоняться. Подобный исход (x*,y*) называется ситуацией равновесия, а принцип оптимальности, основанный на отыскании ситуации равновесия, - принципом равновесия.

Определение. В матричной игре с матрицей 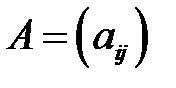размерности 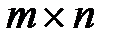исход является ситуацией равновесия или седловой точкой, если

(2.6)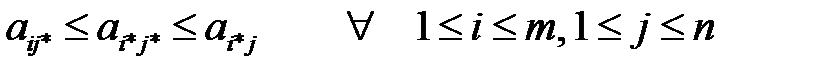

В седловой точке элемент матрицы является одновременно минимумом в своей строке и максимумом в своем столбце. В игре из примера 2 элемент a₃₃ является седловой точкой. Оптимальными в этой игре являются третьи стратегии для обоих игроков. Если первый игрок отклоняется от третьей стратегии, то он начинает выигрывать меньше, чем a₃₃. Если второй игрок отклоняется от третьей стратегии, то он начинает проигрывать больше, чем a₃₃. Таким образом, для обоих игроков нет ничего лучшего, чем последовательно придерживаться третьей стратегии.

Принцип оптимального поведения: если в матричной игре имеется седловая точка, то оптимальным является выбор стратегии, соответствующей седловой точке. Что будет, если в игре окажется более одной седловой точки?

Теорема. Пусть две произвольные седловые точки в матричной игре. Тогда:

(2.7)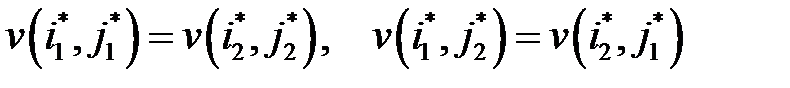

Доказательство. Из определения ситуации равновесия имеем:

(2.8)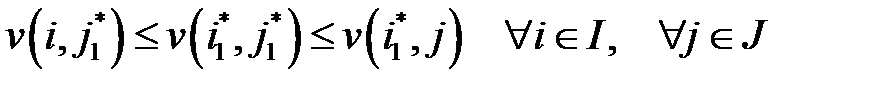

(2.9)

Подставим в левую часть неравенства (2.8) 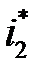, а в правую - 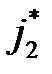, в левую часть неравенства (2.9) - 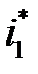, в правую - . Тогда получим:

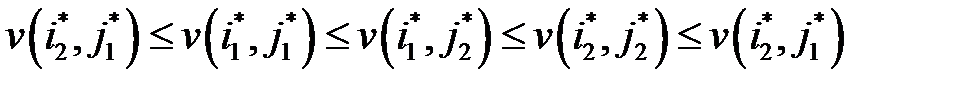
Откуда следует равенство:

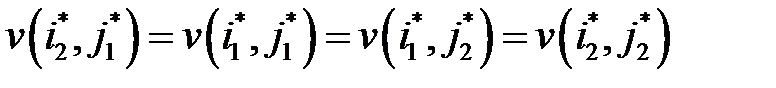
Из теоремы следует, что функция выигрыша принимает одно и то же значение во всех ситуациях равновесия. Именно поэтому число 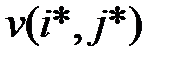называется ценой игры. А стратегии 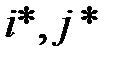, соответствующие любой из седловых точек, называются оптимальными стратегиями игроков 1 и 2, соответственно. В силу (2.7) все оптимальные стратегии игрока взаимозаменяемы.

Оптимальность поведения игроков не изменится, если в игре множества стратегий остаются прежними, а функция выигрыша умножается на положительную константу (или к ней прибавляется постоянное число).

Теорема. Для существования в матричной игре 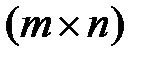cедловой точки (i*,j*) необходимо и достаточно, чтобы максимин был равен минимаксу:

(2.10)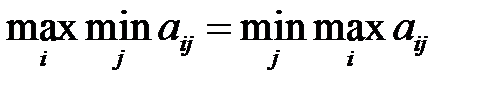

Доказательство. Необходимость. Если (i*,j*) – седловая точка, то, согласно (2.6) :

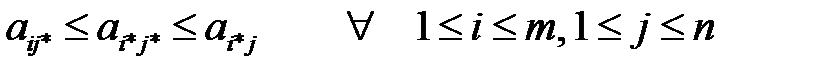
Поэтому

(2.11)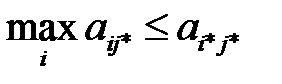

Вместе с тем имеем:

(2.12)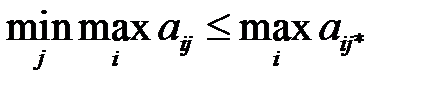

Из (2.11) и (2.12) получаем:

(2.13)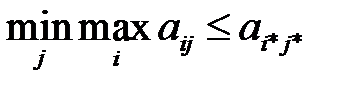

Рассуждая аналогично, приходим к равенствам:

(2.14)

Таким образом,

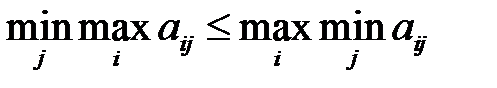
С другой стороны, всегда выполняется обратное неравенство (2.5), поэтому справедливым оказывается (2.10).

Достаточность. Пусть справедливо (2.10). Докажем наличие седловой точки. Имеем:

(2.15)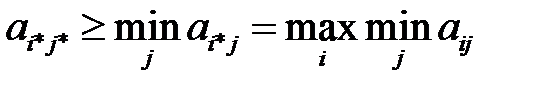

(2.16)

Согласно равенству (2.10), неравенства (2.15) и (2.16) превращаются в равенства. После чего имеем:

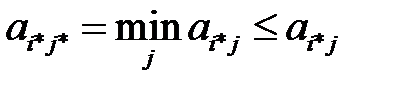
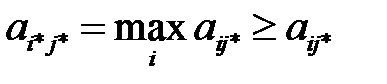
Теорема доказана. Попутно доказано, что общее значение максимина и минимакса равно цене игры .