Доминирование стратегий
Игры размером 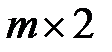 решаются так же, как и игры
решаются так же, как и игры 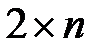 . Для этого достаточно переименовать игроков.
. Для этого достаточно переименовать игроков.
Если минимальный из размеров матрицы больше двух, то решение игры находится методами линейного программирования. В некоторых случаях удается, однако, уменьшить размер матрицы и, тем самым, упростить решение. Уменьшение размеров матрицы производится при помощи приема, основанного на понятии доминирования.
Пусть 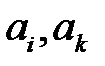 - две строки матрицы игры, а
- две строки матрицы игры, а 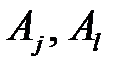 - два ее столбца.
- два ее столбца.
Определение. Говорят, что строка 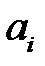 доминирует строку
доминирует строку 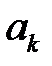 , если
, если 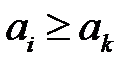 . Говорят, что столбец
. Говорят, что столбец 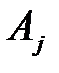 доминирует столбец
доминирует столбец 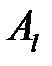 , если
, если 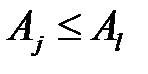 .
.
Вернемся к матрице игры из примера 6. В ней третий столбец покомпонентно меньше второго. Это означает что третья стратегия выгоднее для второго игрока нежели вторая вне зависимости от того, какой выбор сделает первый игрок. Это и означает, что третья стратегия доминирует вторую. Вторая стратегия никогда не будет использоваться вторым игроком. Значит она несущественна и может быть удалена из матрицы игры.
Рассмотрим еще один пример.
Пример 7. Пусть дана матричная игра:
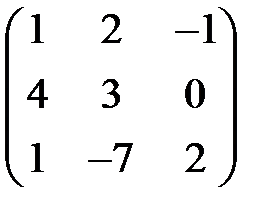
Первая строка покомпонентно меньше второй. Значит, игрок 1 никогда не будет ее применять, и потому матрицу можно упростить, удалив первую строку. В результате получается матрица:
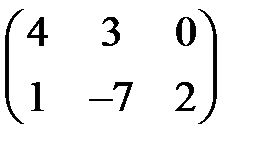
У вновь полученной матрицы первый столбец доминируется вторым, поэтому его тоже можно убрать. Окончательно исходная матрица упрощается до:
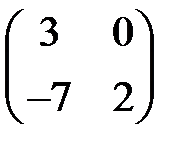
Дата добавления: 2016-10-17; просмотров: 774;
