Диффузия и однородность кристалла

К выступающим частям кристалла — вершинам и ребрам — вещество поступает в большем, чем к серединам граней, количестве, поэтому градиенты концентрации (пересыщения) возникают и вдоль поверхности. Пока размеры кристалла невелики, малы и градиенты пересыщений, кристалл обычно растет плоскогранным. Причина этого заключается в том, что слои роста имеют повышенные скорости продвижения по поверхности по сравнению со скоростью возникновения новых слоев (§ 1.5). Однако с увеличением кристалла градиенты пересыщений вдоль грани нарастают. Теперь уже могут возникнуть условия, при которых вновь возникший слой не успеет распространиться по всей грани, приреберные участки обгонят в своем росте центральные участки грани, в ней возникнет углубление (рис. 1-21).При росте кристалла до некоторых размеров оно периодически перекрывается слоем вновь нарастающего вещества, так что в кристалле образуется серия уплощенных включений раствора, расположенных друг под другом. Может образоваться и одиночное включение раствора. Такие включения, занимающие сравнительно большую площадь, будем называть «площадными».

Неравномерность диффузии может приводить к тому, что слои по поверхности кристалла также будут распространяться неравномерно и иметь в результате извилистые торцы (такая форма ступеней возникает иногда и по другой причине — см. рис. 1-25). За впадинами торцов в кристалле тогда будут оставаться мелкие — «точечные» («цепочечные») включения раствора. По мере дальнейшего увеличения размера кристалла продолжают увеличиваться градиенты пересыщений вдоль грани, и наступает такой момент, когда захоронения включений не происходит, в кристалле образуется воронка (рис. 1-21). Кристалл с воронками-провалами в гранях называется «реберным скелетом». При нарастании неравномерности пересыщения происходит разрыв и ребер — кристалл превращается в «вершинный скелет» (рис. 1-22). Подчеркнем, что скелетный кристалл имеет единую непрерывную кристаллическую структуру в любом своем участке в отличие от дендрита (§ 1.8).

Из сказанного понятно, почему включения раствора возникают в первую очередь в пирамидах роста быстрорастущих граней.

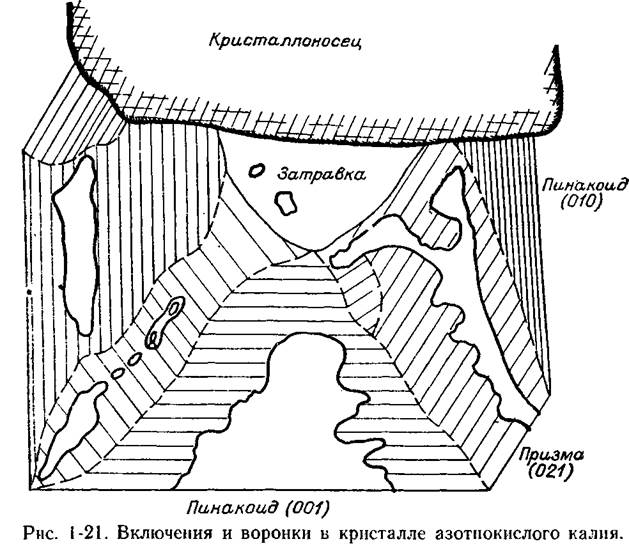
Последовательные стадии роста кристалла зафиксированы киносъемкой (интервал между кадрами 2 мин). Штрихами показана граница между пирамидами роста. Наложивишеся друг на друга контуры включения в пирамиде роста грани (021) — изменения в форме и размерах одного и того же включения в процессе роста. Размер кристалла около 1,5 мм, температура опыта 72° С, переохлаждение раствора 0,75° С. Рост в режиме свободной конвекции, в водном растворе, головкой вниз.

Например, на рис. 1-21противоположные грани одного и того же пинакоида (010) растут с разной скоростью; включения раствора имеются в грани с большей скоростью роста (слева).

Иногда образованию включений раствора или скелетному росту предшествует также образование толстых, различимых невоору­женным глазом слоев. Серия таких толстых слоев может привести к ступенчатости грани. Ступенчатость, образованная прямолиней­ными ступенями, бывает довольно сложной по профилю (одно­сторонней, двусторонней и т. д.) и называется в данном случае диффузионной штриховкой.

Включения раствора, скелетный рост, толстые слои на гранях и диффузионная штриховка — признаки заметного диффузионного влияния среды.

Чем больше пересыщение, тем при меньших размерах кристал­лов происходят переходы к скелетным формам. В отношении этих явлений разные вещества ведут себя крайне индивидуально. Так, хлористый аммоний (рис. 1-22) растет таким практически при лю­бых, даже самых малых доступных пересыщениях и очень малых размерах кристалла. В то же время, например, алюмокалиевые квасцы неохотно дают включения раствора и тем более скелетные кристаллы и образуют прекрасные крупные кристаллы в широкой области пересыщений.

В разных диффузион­ных режимах вероятность
возникновения описанных
особенностей кристаллов
различна. В режиме мо­лекулярной диффузии
только малые пересыще­ния могут привести к рос­ту полногранных кристал­лов ввиду малых скоростей диффузии. В режиме
свободной конвекции

меньше градиенты кон­центраций вдоль граней из-за конвекционных по­токов и из-за того, что скорости диффузии боль­ше. Это позволяет получить однородные кристаллы при сущест­венно больших пересыщениях (скоростях роста), чем в предыду­щем режиме. В режиме вынужденной конвекции в связи с повы­шением скорости течения раствора и уменьшением толщины диффузионного слоя скорости диффузии еще больше, а градиенты пересыщений вдоль грани еще меньше, что дает возможность от­носительно быстро выращивать крупные однородные кристаллы, получение которых при других режимах затруднительно.

Имеется формула, которая описывает скорость диффузии ве­щества к грани, расположенной параллельно ламинарному (по­слойному, упорядоченному) потоку жидкости, в которой находится кристалл [Лыков А. В., 1978 г.]:

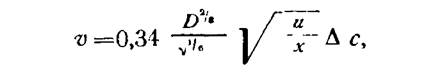
где D — уже упоминавшийся коэффициент диффузии; υ — кинема­тическая вязкость раствора; и — скорость движения раствора от­носительно кристалла; ∆ с — пересыщение; х — расстояние вдоль грани от переднего ребра, где раствор набегает на кристалл, до точки, для которой производят расчет. Как видно из формулы, скорость диффузии к грани падает при удалении от ребра, встре­чающего поток. Эта формула описывает ту скорость диффузии, ко­торая имела бы место, если бы кристалл усваивал все поступаю­щее к нему вещество и повсеместно по поверхности кристалла сохранялась бы одинаковая концентрация раствора, равная кон­центрации насыщения (т. е. если бы был чисто диффузионный ли­мит скорости роста).

Зная скорость роста грани при данном пересыщении, по этой формуле можно рассчитать, на каком расстоянии от переднего ребра (т. е. при каком приблизительно размере кристалла) ско­рость диффузии окажется лимитирующей, раствор истощится и на грани возникнет углубление. Или, например, зная скорость роста и размер кристалла, можно рассчи­тать, при какой скорости движения жидкости исчезнут включения раст­вора.

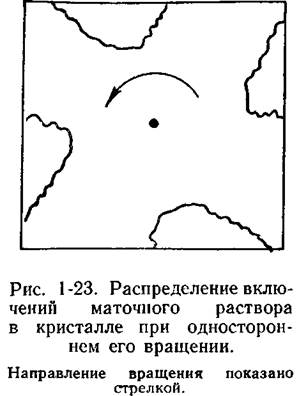
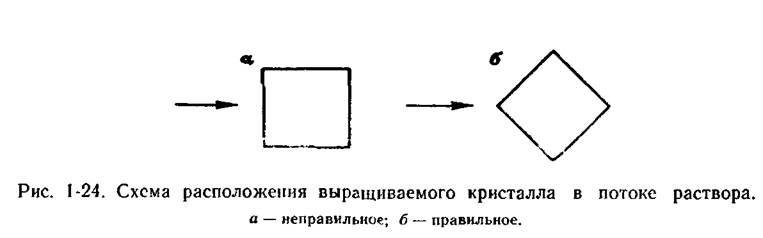
Подобную формулу (с несколь­ко отличным числовым коэффициен­том при формуле) для анализа про­цесса образования включений раство­ра в кристаллах впервые использовал А. Карлсон. Рассчитанная им по ука­занной формуле скорость движения раствора, обеспечивающая однород­ность кристаллов КН₂Р0₄ и NH₄H₂P0₄, равна 9 см/с. Результат эксперимента, проведенного А. Карлсоном (10— 15 см/с), можно считать удовлетвори­тельным. В дальнейшем систематиче­ские исследования в этом направлении [Трейвус Е. Б., 1979] подтвердили воз­можность указанного подхода к захвату включений раствора в режиме не только вынужденной, но и свободной конвекции. Подчеркнем, что приведенное выше уравнение справедливо только для гладкой грани, параллельной потоку. При появлении у переднего ребра макроскопической ступени можно ожидать воз­никновения турбулизации (завихрений) раствора за ней, т. е. уве­личения перемешивания раствора, и некоторого не предусмотрен­ного в формуле увеличения скорости диффузии. Формула непри­менима к тыльным по отношению к потоку граням кристалла. Около этих граней легко образуется застойная зона раствора, и в них наиболее часто возникают включения. Так, при вращении кристалла застойная зона образуется за передним ребром грани (рис. 1-23), здесь по мере роста кристалла раствор обедняется ве­ществом. Участок грани вблизи застойной зоны оказывается в условиях относительного «голодания». На грани возникает углубление и затем включение. Поэтому при выращивании необ­ходимо располагать кристалл так, чтобы поток в наилучшей сте­пени обтекал кристалл (рис. 1-24).

В одном и том же кристалле включения раствора в пирамидах роста одних граней могут возникать, а в других нет, хотя скорости роста этих граней приблизительно равны и прочие условия роста приблизительно одинаковы. Для объяснения этого явления пред­лагалось [Петров Т. Г., 1964] учесть особенности состояния рас­твора вблизи поверхности кристалла.

Поскольку существует упорядоченный слой жидкости на грани, в котором подвижность молекул снижена по сравнению с их по­движностью вдали от кристалла, то коэффициент диффузии крис­таллизуемого вещества в этом слое должен быть меньше, чем в объеме раствора. Так как ориентирующее влияние разных гра­ней на раствор в принципе разное, неодинаковым будет и коэффи­циент диффузии у разных граней в адсорбционном слое.

В этом можно видеть объяснение того, почему для кристаллов азотнокис­лого калия частоты образования включений раствора в разных пирамидах роста при сходных скоростях их нарастания хорошо согласуются со степенью сходства атомарного рисунка разных граней кристаллов и базисной грани льда [Петров Т. Г., 1964], т. е. включения возникают чаще при большем сходстве рисунков. Сход­ство рисунков — косвенный признак того, что данная грань обла­дает большим ориентирующим действием на растворитель.

При повышении температуры скорость межфазной стадии воз­растает быстрее, чем скорость диффузии. Таким образом, с повы­шением температуры должны возрастать диффузионное влияние на рост кристалла, вероятность возникновения включений, скелет­ного роста, появления толстых слоев на гранях. Тем не менее, час­тота образования включений, например на некоторых гранях крис­таллов нитрата калия, с температурой уменьшается. Для объясне­ния указанного факта можно привлечь уже изложенные представ­ления о существовании адсорбционного слоя раствора на грани. Поскольку повышение температуры ослабляет химические связи в адсорбционном слое, следствием этого является уменьшение ориентирующего действия поверхности кристалла на раствор, спе­цифическое (зависящее от конкретной грани) уменьшение тол­щины этого слоя, короче говоря, десольватация грани. Видимо, этот процесс идет с повышением температуры достаточно интен­сивно, что и вызывает уменьшение частоты возникновения включе­ний раствора. Другая возможная причина уменьшения частоты возникновения включений может заключаться в так называемом недиффузионном захвате материала, обусловленном тем, что крис­талл при росте занимает пространство, часть которого уже была занята веществом, находившимся в растворе и непосредственно использованном на постройку кристалла. Так как с повышением температуры концентрация раствора увеличивается, то увеличи­вается и часть объема, занятая этим веществом. Соответственно уменьшается и роль объемной диффузии. Роль недиффузионного захвата в уменьшении частоты возникновения включений может быть особенно заметна для нитрата калия, растворимость которого сильно возрастает с температурой.

Отметим, что специфическую десольватацию кристалла, т. е. разупорядочение и утоньшение адсорбционного слоя, следует ожи­дать, согласно В. Клеберу, и при повышении пересыщения.

Однако в этом случае, видимо, быстрее нарастают градиенты концентраций вдоль граней и потому число включений раствора в кристал­лах все-таки с пересыщением возрастает.

На объемную диффузию и диффузию в упорядоченном слое раствора вблизи грани могут оказывать влияние примеси. Увели­чение скорости диффузии должно происходить в присутствии час­тиц, обладающих десольватирующим эффектом, например Н⁺ и ОН^-. Действительно, по нашим данным, скорости роста кристаллов KNO₃ в присутствии избытка ионов Н⁺ или ОН^- увеличиваются. Так как это вещество не подвергается гидролизу и указанные ионы, согласно правилу Панета (§ 1.7), не должны заметно адсор­бироваться азотнокислым калием, то их воздействие можно объ­яснить увеличением скорости диффузии как в объеме раствора, так и в адсорбционном слое. Заметим, однако, что во многих случаях ионы Н⁺ и ОН^- обнаруживают десольватирующий эффект только при сравнительно небольшой их концентрации в растворе. При их больших концентрациях нередко преобладают эффекты комплексообразования, что приводит к уменьшению скоростей роста.